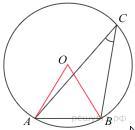
Найдите хорду, на которую опирается угол 30°, вписанный в окружность радиуса 3.

1 ответ

Посмотреть ответы

Megamozg

2200

Ответ:3

Заметим, что угол ACB=30°. Значит, угол AOB=60° , т. к. является центральным углом, опирающимся на ту же хорду. Соответственно, треугольник AOB — равносторонний, так как AO = OB = AB = R = 3.

Хороший ответ

29 декабря 2022 12:54

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Найдите sin альфа, если cos альфа равен 2\3... В прямоугольном треука высота, проведенная из вершины прямого угла, равна медиане, проведенной из того же угла. Гипотенуза этого треука равна 6, найти... найдите высоту прямоугольного треугольника проведенную из вершины прямого угла если она делит гипотенузу на отрезки длиной 9 и 25 см... радиус окружности, вписанной в правильный шестиугольник, равен 3 см. найдите радиус окружности, описанной около данного шестиугольника... основанием пирамиды с вершиной о является параллелограмм abcd. Разложите вектор od по векторам a= oa b= ob c=oc...

Най­ди­те хорду, на ко­то­рую опи­ра­ет­ся угол 30°, впи­сан­ный в окруж­ность ра­ди­у­са 3.​

Найдите хорду, на которую опирается угол 30°, вписанный в окружность радиуса 3.