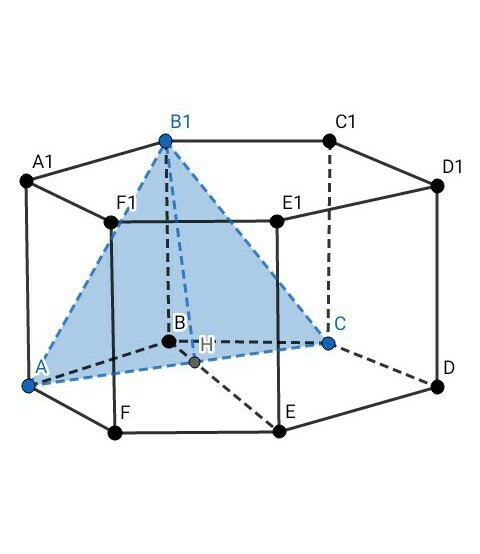
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра которой равны 1, найдите расстояние от точки A до прямой CB1.

ДАНО: АВСDEFA1B1C1D1E1F1 - правильная шестиугольная призма ; АВ = АА1 = 1

НАЙТИ: p ( A ; CB1 )
_________________________

РЕШЕНИЕ:

1) точка А и отрезок СВ1 лежат в плоскости треугольника АВ1С.

Все боковые грани правильной шестиугольной призмы равны.
Значит, АВ1 = В1С => ∆ АВ1С - равнобедренный

Найдём все стороны ∆ АВ1С

2) Рассмотрим ∆ АВ1В ( угол АВВ = 90° ):

По теореме Пифагора:

АВ1² = АВ² + ВВ1²

АВ1² = 1² + 1² = 2

АВ1 = √2

АВ1 = В1С = √2

3) В основании правильной шестиугольной призмы лежит правильный шестиугольник. Все углы правильного шестиугольника равны 120°.

Рассмотрим ∆ АВС ( АВ = ВС ):

По теореме косинусов:

АС² = АВ² + ВС² - 2 × АВ × ВС × cos ABC

AC² = 1² + 1² - 2 × 1 × 1 × cos 120°

AC² = 2 - 2 × ( - 1/2 ) = 2 + 1 = 3

AC = √3

4) B1B перпендикулярен ВН
ВН перпендикулярен АС

Значит, по теореме о трёх перпендикулярах В1Н перпендикулярен АС

Высота в равнобедренном ∆ АВ1С является и медианой и биссектрисой =>

АН = НС = 1/2 × АС = 1/2 × √3 = √3/2

5) Рассмотрим ∆ В1СН ( угол В1НС = 90° ):

По теореме Пифагора:

В1С² = В1Н² + НС²

В1Н² = ( √2 )² - ( √3/2 )² = 2 - 3/4 = 5/4

В1Н = √5/2

Опустим из точки А перпендикуляр АМ на отрезок В1С. Соответственно, АМ = р ( А ; В1С )

6) Найдём площадь ∆ В1АС:

S b1ac = 1/2 × AC × B1H

С другой стороны, S b1ac = 1/2 × B1C × AM

Приравняем площади и получим:

1/2 × АС × В1Н = 1/2 × В1С × АМ

АС × В1Н = В1С × АМ

АМ =


Значит, p ( А ; В1С ) = √30/4



ОТВЕТ: √30 / 4