Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
14 января 2023 23:38
793
Помогите решить уравнение
cosx=корень из 2/2. И остальные по порядку
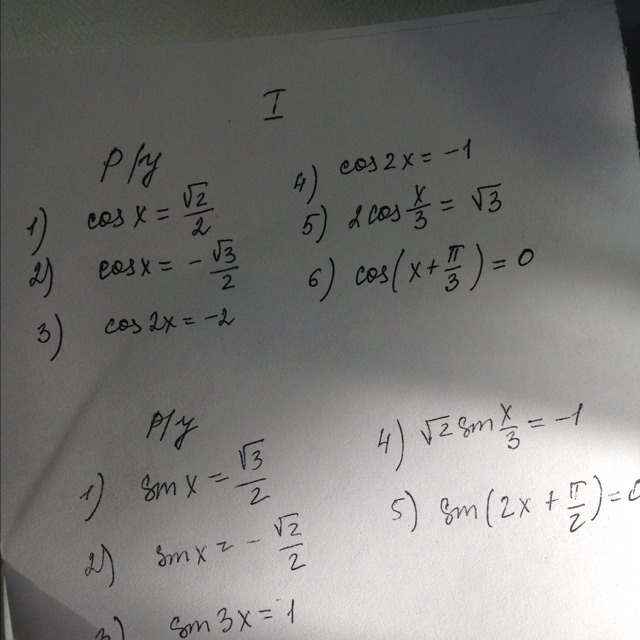
1
ответ
Нужно уметь решать простейшие тригонометрические уравнения:
1) cos x = a
x = ±arccos a + 2πn, n ∈ Z (|a| ≤ 1);
2) sin x = a
x = (-1)ⁿ · arcsin a + πn, n ∈ Z (|a| ≤ 1).
I.
1) cos x = √2/2, x = ±π/4 + 2πn, n ∈ Z;
2) cos x = -√3/2, x = ±5π/6 + 2πn, n ∈ Z;
3) cos x = -2, нет решений, т.к. |-2| > 1;
4) cos 2x = -1,
2x = π + 2πn, n ∈ Z,
x = π/2 + πn, n ∈ Z;
5) 2cos (x/3) = √3,
cos (x/3) = √3/2,
x/3 = ±π/6 + 2πn, n ∈ Z;
x = ±π/2 + 6πn, n ∈ Z;
6) cos(x + π/3) = 0,
x + π/3 = π/2 + πn, n ∈ Z,
x = π/2 - π/3 + πn, n ∈ Z,
x = π/6 + πn, n ∈ Z;
1) sin x = √3/2,
x = (-1)ⁿ · π/3 + πn, n ∈ Z;
2) sin x = -√2/2,
x = (-1)ⁿ · (-π/4) + πn, n ∈ Z,
x = (-1)ⁿ⁺¹ · π/4 + πn, n ∈ Z;
3) sin 3x = 1,
3x = π/2 + 2πn, n ∈ Z,
x = π/6 + 2πn/3, n ∈ Z;
4) √2sin(x/3) = -1,
sin(x/3) = -1/(√2),
sin(x/3) = -√2/2,
x/3 = (-1)ⁿ · (-π/4) + πn, n ∈ Z,
x/3 = (-1)ⁿ⁺¹ · π/4 + πn, n ∈ Z,
x = (-1)ⁿ⁺¹ · 3π/4 + 3πn, n ∈ Z;
5) sin(2x + π/2) = 0,
2x + π/2 = πn, n ∈ Z,
2x = -π/2 + πn, n ∈Z,
x = -π/4 + πn/2, n ∈ Z.
1) cos x = a
x = ±arccos a + 2πn, n ∈ Z (|a| ≤ 1);
2) sin x = a
x = (-1)ⁿ · arcsin a + πn, n ∈ Z (|a| ≤ 1).
I.
1) cos x = √2/2, x = ±π/4 + 2πn, n ∈ Z;
2) cos x = -√3/2, x = ±5π/6 + 2πn, n ∈ Z;
3) cos x = -2, нет решений, т.к. |-2| > 1;
4) cos 2x = -1,
2x = π + 2πn, n ∈ Z,
x = π/2 + πn, n ∈ Z;
5) 2cos (x/3) = √3,
cos (x/3) = √3/2,
x/3 = ±π/6 + 2πn, n ∈ Z;
x = ±π/2 + 6πn, n ∈ Z;
6) cos(x + π/3) = 0,
x + π/3 = π/2 + πn, n ∈ Z,
x = π/2 - π/3 + πn, n ∈ Z,
x = π/6 + πn, n ∈ Z;
1) sin x = √3/2,
x = (-1)ⁿ · π/3 + πn, n ∈ Z;
2) sin x = -√2/2,
x = (-1)ⁿ · (-π/4) + πn, n ∈ Z,
x = (-1)ⁿ⁺¹ · π/4 + πn, n ∈ Z;
3) sin 3x = 1,
3x = π/2 + 2πn, n ∈ Z,
x = π/6 + 2πn/3, n ∈ Z;
4) √2sin(x/3) = -1,
sin(x/3) = -1/(√2),
sin(x/3) = -√2/2,
x/3 = (-1)ⁿ · (-π/4) + πn, n ∈ Z,
x/3 = (-1)ⁿ⁺¹ · π/4 + πn, n ∈ Z,
x = (-1)ⁿ⁺¹ · 3π/4 + 3πn, n ∈ Z;
5) sin(2x + π/2) = 0,
2x + π/2 = πn, n ∈ Z,
2x = -π/2 + πn, n ∈Z,
x = -π/4 + πn/2, n ∈ Z.
0
·
Хороший ответ
16 января 2023 23:38
Остались вопросы?
Еще вопросы по категории Алгебра
3 в 7 степени *11 в 7 степени /33 в 6 степени...
Преобразуй трёхчлен 18*x*y+y2+81*x2 2 это степень Ответы 1.(9*x)2-y2 2.y2-(9*x)2 3.(9*x-y)2 4.(y-9*x)2 5.(y+9*x)2 нужно выбрать ответ...
Log 2 x+log2(x-7)=3 решить...
Sin pi(x-3)/6=-0,5 найти наименьший положительный корень...
Помогите с уравнением 4sinx+5cosx=4...