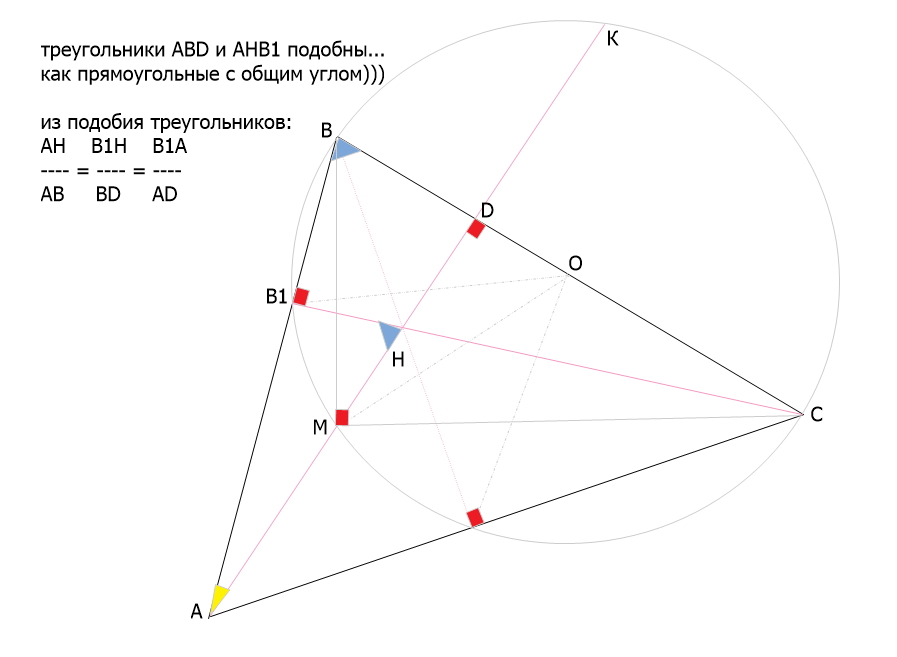
На стороне BC остроугольного треугольника ABC ( AB≠AC ) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=85, MD=68, H — точка пересечения высот треугольника ABC. Найдите AH.

1 ответ

Посмотреть ответы

DevAdmin

1720

Треугольники ABD и AHB1 подобны ⇒
АН = АВ*АВ1 / AD
треугольник ВМС будет прямоугольным (он опирается на диаметр)))
MD² = BD*DC
по теореме о секущих АВ*АВ1 = AK*AM
по свойству хорд MD*DK = BD*DC = MD² ⇒
DK = MD
AK = AD + DK = AD + MD
AM = AD - MD
и тогда
AH = (AD + MD)*(AD - MD) / AD = (AD² - MD²) / AD = AD - MD² / AD
AH = (85+68)*(85-68) / 85 = 153*17 / (5*17) = 153 / 5 = 306 / 10 = 30.6

Хороший ответ

17 января 2023 01:20

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

В основании правильной пирамиды MABCD лежит квадрат ABCD. Hайдите расстояние от центра грани ABCD до ребра MC, если высота пирамиды равна 6, а длина р... В равнобедренном треугольнике с основанием 12см проведена высота 9см. Найдите радиус окружности, вписанной в треугольник.... Найдите площадь треугольника,вершины которого имеют координаты (1;0),(11;7),(8;10). Пожалуйста с решением. Заранее спасибо.... Помогите с решением!! В равнобедренной трапеции известна высота большее основание и угол при основании найдите меньшее основание трапеция на рисунке... Найдите площадь прямоугольника,если его диагональ равная 10 см, образует со стороной угол, равный 30*(*-градусам)...