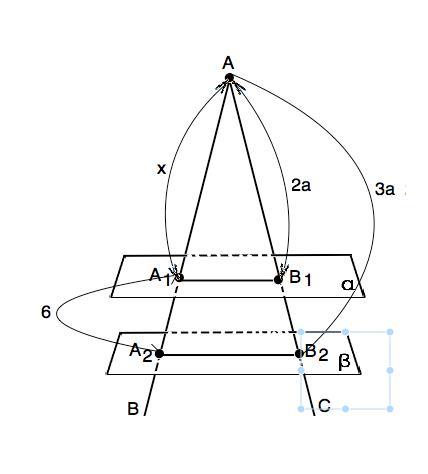
Параллельные плоскости альфа и бета пересекают сторону АВ угла ВАС соответственно в точках А1 и А2, а сторону АС этого угла в В1 и В2. Найти АА1 если А1А2=6, АВ2:АВ1=3:2 ? помогите срочно нужно

1 ответ

Посмотреть ответы

DevAdmin

1720

Ответ: 12 (ед. длины)
Объяснение:
Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. ⇒ А1В1║А2В2
Стороны угла – секущие при параллельных А1В1 и А2В2, ⇒ соответственные углы при их пересечении равны.
Треугольники АА1В1 и АА2В2 подобны по трем углам.
Примем АА1=х Тогда АА2=х+6 .
Из подобия треугольников АА2 и АА1 следует отношение:
(х+6):х=3:2
3х=2х+12
х=12
АА1=12 (ед. длины)

Хороший ответ

17 января 2023 03:04

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Прямая ЕК является секущей для прямых CD и MN (E пренадлежит СD, K пренадлежит MN) Угол DEK равен 65°. При каком значении угла NKE прямые CD и MN могу... Квадрат вписан в окружность диаметра 8. Периметр квадрата равен: 1) 32 2)16 2^ 3)16 4) 32 2^... 1) На данном рисунке OC- биссектриса угла AOB, угол 1= 128 градуса, угол 2= 52 градуса. а) Докажите, что AO=AC б) Найдите угол ACO 2) Дан угол ABC, ра... Напишите пожалуйста решение этого задания . Найдите косинус угла между векторами  а  = 4m – p и  b  = m + 2p, если m ⊥ p и m... Как начертить сумму неколлинеарных вектора...