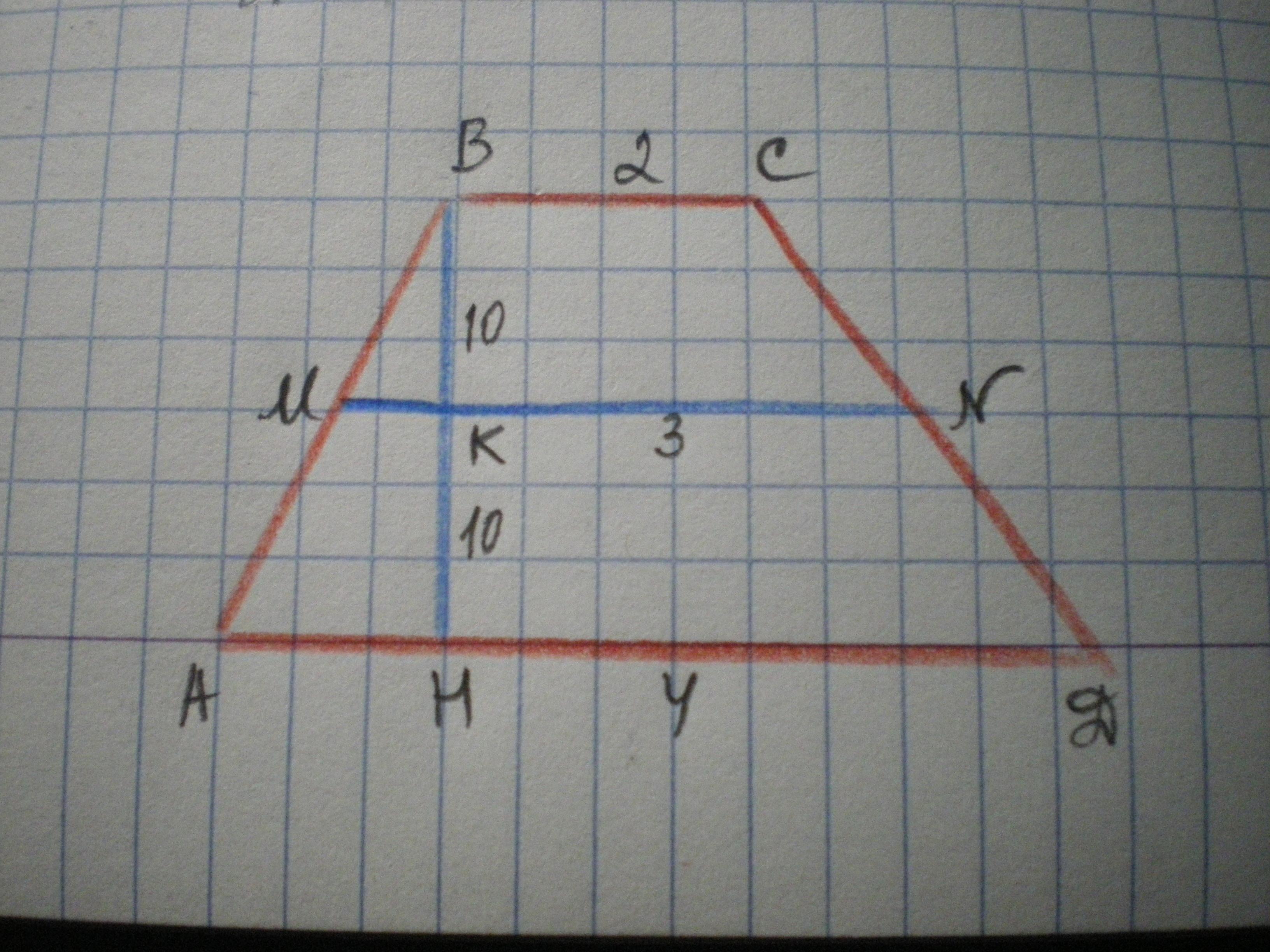
В трапеции ABCD известно,что AD=4,BC=2,а ее площадь равна 60.Найдите площадь трапеции BCNM,где MN-средняя линия трапеции ABCD.

1 ответ

Посмотреть ответы

Megamozg

2205

Ответ:
25 см²
Пошаговое объяснение:
Дано: ABCD - трапеция, AD=4 см, BC=2 см, S=60 см², МN - средняя линия. Найти S(BCNM).

Решение: МN=(АD+ВС)/2=(2+4)/2=3 см.
Проведем высоту ВН. Найдем ВН из формулы S=MN*BH
60=3ВH; BH=20 cм.
Найдем S(BCNM)=(ВС+MN)/2 * ВК.
ВК=1/2 ВН, т.к. MN - средняя линия и делит ВН пополам.
ВК=20:2=10 см.
S(BCNM)=(2+3)/2 * 10 = 25 см²

Хороший ответ

17 января 2023 06:22

Остались вопросы?

Найти нужный

Еще вопросы по категории Математика

3.ядро ²¹⁶/⁸⁴pо образовано после двух последовательных а-распадов. ядро полония образовано ядром скелета?... Как делить в столбик?... Может ли 1 м3 быть равен 1 см3?... Какое действие нужно выполнить с числами 1 и 2, чтобы получить результат умножения на 12?... решите неравенство: √x^2-9(x^2-4x+4)<=0...