1)решите неравенство используя метод интервалов: а) (x+9)(x-5)>0 б) x-3/x+6<02)решите уравнение: а)x^3-49x=0 б)x^2+3/4-17-3x/8=2 в) x^4-17x^2+16=0
3)при каких значениях t уравнение 25x^2+tx+1=0 не имеет корней?
4) найти область определения функции y=корень5x-2x^2

1 ответ

Посмотреть ответы

DevAdmin

1720

Задание 1. - вложение 1
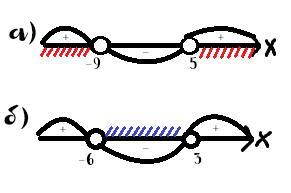
а) (x+9)(x-5)>0
f(x)=(x+9)(x-5)
Нули функции: -9; 5
Ответ: (-∞; 9)∪(5; +∞)
б)
$\frac$
ОДЗ: x≠-6
(x-3)(x+6)<0
f(x)=(x-3)(x+6)
Нули функции: 3; -6
Ответ: (-6; 3)
Задание 2.
а)
x³ - 49x = 0
x(x²-49)=0
x(x-7)(x+7)=0
x=0 или x=7 или x=-7
Ответ: -7; 0; 7
б)
$\frac-\frac=2|*8\\\\2(x^2+3)-17+3x=16\\2x^2+6-17+3x-16=0\\2x^2+3x-27=0\\D=3^2-4*2*(-27)=225\\x_1=\frac{-3-\sqrt}=\frac{-3-15}=\frac{-18}=-4,5\\\\x_2=\frac{-3+\sqrt}=\frac{-3+15}=\frac=3$
Ответ: -4,5; 3
в) x⁴ - 17x² + 16 = 0
x² = t - новая переменная
$t^2 - 17t + 16 = 0\\D =(-17)^2-4*1*16=289-64=225\\t_1==\frac}=\frac=\frac=1\\\\t_2==\frac}=\frac=\frac=16$
x² = 1 или x² = 16
x₁=-1 ; x₂=1 ; x₃=-4 ; x₄=4
Ответ: ±1; ±4
Задание 3. - вложение 2
D < 0, корней нет
$25x^2+tx+1=0\\D=t^2-4*1*25=t^2-100\\\\t^2-100$
Нули функции: 10; -10
Ответ: t∈(-10; 10)
Задание 4. - вложение 3
$y=\sqrt\\\\5x-2x^2 \geq 0\\x(5-2x)\geq0\\f(x)=x(5-2x)$
Нули функции: 0; 2,5
Ответ: x∈[0; 2,5]

Хороший ответ

17 января 2023 07:32

Остались вопросы?

Найти нужный

Еще вопросы по категории Алгебра

Б) найдите все значения р, при которых неравенство не имеет решений. х^2-(2p+2)x+3p+7< или = 0... 9y-4/y+2=y+8/y+2 Решите уравнение пожалуйста... Начертите неразвернутый угол АОВ и проведите:а)луч OC,который делит угол AОВ на два угла :б) луч OD, который не делит угол АОС на два угла... Решить уравнение : а) 2x-3(x-1)=4+2(x-1); б) x/3 + x+1/4 = 2... Трактор едет по дороге проезжая 10 м каждую секунду. Выразите скорость трактора в километров на час...