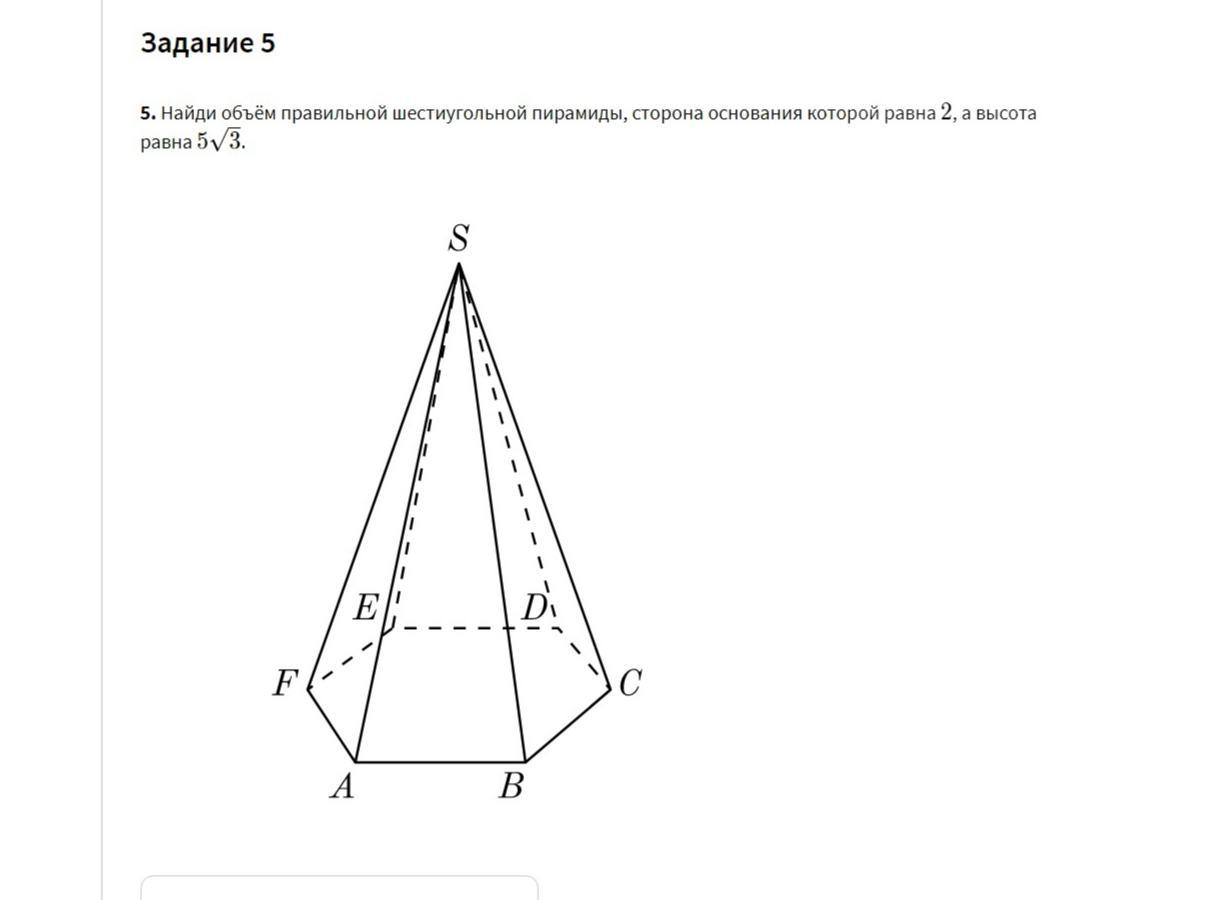
Найдите объем правильной шестиугольной пирамиды, сторона основания которой равна 2, а высота равна 5√3помогите, пж

1 ответ

Посмотреть ответы

DevAdmin

1690

Ответ:
30 куб. ед.
Пошаговое объяснение:
Объем пирамиды вычисляется по формуле:
$V= \dfrac \cdot S\cdot H,$
где S- площадь основания пирамиды, а H- высота.
По условию $H=5\sqrt$ ед. Найдем площадь основания. В основании пирамиды правильный шестиугольник.
Площадь правильного шестиугольника определяется по формуле
$S= \dfrac\sqrt } ;\\\\S=\dfrac\cdot \sqrt } =\dfrac } =\dfrac }=6\sqrt3}$
Площадь основания пирамиды 6√3 кв. ед.
Тогда объем пирамиды будет
$V=\dfrac \cdot 6\sqrt \cdot 5\sqrt =2\sqrt \cdot5\sqrt =10\cdot3=30$ куб. ед.

Хороший ответ

17 января 2023 10:13

Остались вопросы?

Найти нужный

Еще вопросы по категории Математика

Что нужно сделать с числом 25 в задании?... Найдите sin(a) если cos(a) = 0,6 и Пи < a < 2Пи... Какая площадь соответствует 1 квадратному дециметру?... Куб разности чисел 9 и 8 Квадрат суммы чисел 8 и 7 Сумма квадратов чисел 8и 7... Половина задуманного числа на 70 больше седьмой части самого задуманного числа. Найдите задуманное число. Помогите пж!!!...