Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
15 января 2023 11:44
10761
Исследуйте функцию и постройте её график f(x)=x^4-2x^2
1
ответ
Исследуйте функцию и постройте её график f(x)=x⁴-2x²
1) Область определения и область значения
Ограничений нет. Значит D(f)=R. E(f)=R
2) точки пересечения с осями координат

__+___-√2__-___0__-___ √2__+___
f(x)>0 f(x)<0 f(x)<0 f(x)>0

точки пересечения с Оу (0;0)
точки пересечения с Ох (0;0); (-√2;0) (√2;0)
3) четность или нечетность

функция четная
4) точки максимума и минимума


__-___ -1 ____+_____0__-__-1___+___
убывает/ возрастает/ убывает/ возрастает
Значит х=-1 и х=1 точки минимума
х=0 точка максимума
f(-1)=f(1)=-1
f(0)=0
5) точки перегиба


___+____ - 1/√3____-______1/√3___+_
вогнутая выпуклая вогнутая
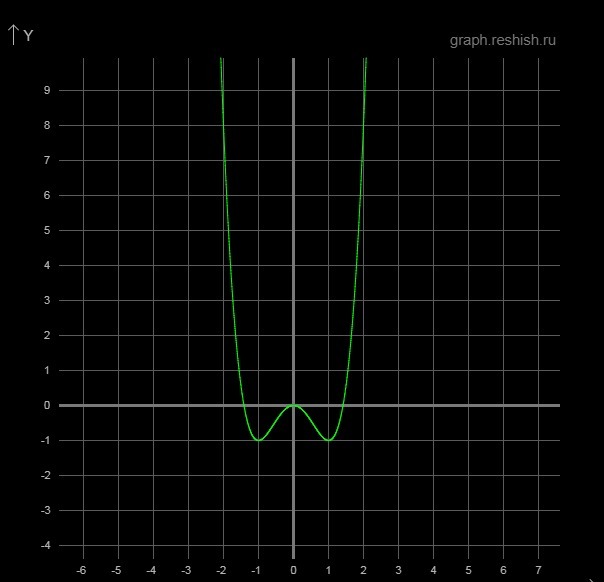
И график в приложении
1) Область определения и область значения
Ограничений нет. Значит D(f)=R. E(f)=R
2) точки пересечения с осями координат
__+___-√2__-___0__-___ √2__+___
f(x)>0 f(x)<0 f(x)<0 f(x)>0
точки пересечения с Оу (0;0)
точки пересечения с Ох (0;0); (-√2;0) (√2;0)
3) четность или нечетность
функция четная
4) точки максимума и минимума
__-___ -1 ____+_____0__-__-1___+___
убывает/ возрастает/ убывает/ возрастает
Значит х=-1 и х=1 точки минимума
х=0 точка максимума
f(-1)=f(1)=-1
f(0)=0
5) точки перегиба
___+____ - 1/√3____-______1/√3___+_
вогнутая выпуклая вогнутая
И график в приложении
0
·
Хороший ответ
17 января 2023 11:44
Остались вопросы?
Еще вопросы по категории Алгебра
Вычислите: а) 2 sin 60°•ctg 60°; в) 7 tg30°•ctg 30°; б) 2 sin 45° - 4 cos 30°; r) 6 ctg 60°- 2 sin 60°....
Логарифм в квадрате х по основанию 3 минус ➖ 2логарифм х по основанию 3 =3...
Укажите приближённое значение числа b, равное среднему арифметическому приближений с недостатком и избытком, если 5,8≤b≤6,4. Ответ округлите до целых....
Буду очень благодарна....
1+sin^2x+cosx=0 решите пожалуйста...