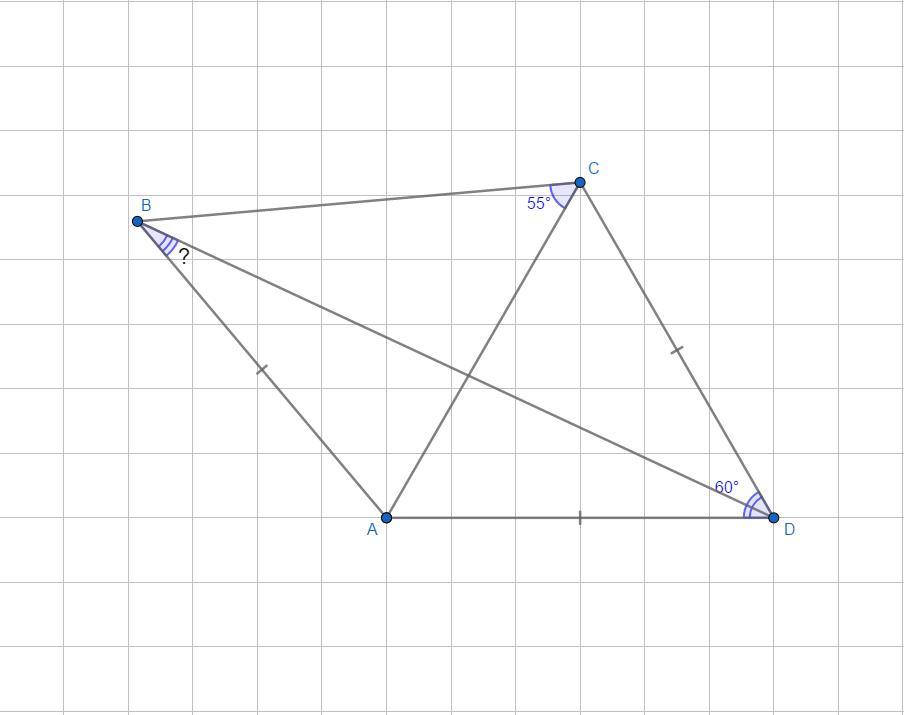
В выпуклом четырёхугольнике ABCD известно что угол ADC равен 60 градусов и AB = AD=DC найдите ABD если известно угол BCA= 55 градусов

1 ответ

Посмотреть ответы

DevAdmin

1700

Ответ:

∠ABD=25°

Объяснение:

В равнобедренном треугольнике углы при основании равны.
Теорема о сумме углов треугольника: Сумма углов треугольника равна 180°.
Если в треугольнике три угла равны, то такой треугольник равносторонний.

1) ΔADC - равнобедренный, т.к. AD=DC по условию, тогда $\displaystyle \boldsymbol{\angle CAD=\angle ACD}=\frac =\frac =\boldsymbol.$
Получили, что ∠ADC=∠CAD=∠ACD=60°, значит, ΔADC - равносторонний, тогда AD=DC=AC=AB.
2) ΔBAC - равнобедренный, т.к. AC=AB, тогда ∠CBA=∠BCA=55°.
Из т. о сумме углов треугольника: ∠BAC=180°-∠CBA-∠BCA=180°-55°-55°=70°.
3) ΔBAD - равнобедренный, т.к. AB=AD по условию, тогда $\displaystyle \boldsymbol{\angle ABD}=\angle ADB=\frac =\frac =\\=\frac=\frac =\boldsymbol.$

Хороший ответ

17 января 2023 11:50

Остались вопросы?

Найти нужный

Еще вопросы по категории Математика

Значение какого из выражений являются рациональным числом? 1)√6-3 2)√3*√5 3)(√5)2(двойка маленькая на верху, просто не знаю как там писать) 4)(√6-3)2... Составь задачу по чертежу и реши ее: 60км/ч, 70 км/ч, 90 км... Найди площадь фигур 5м 4м 3м 2м 4м 6м... Что произошло на Руси в 1093 году?... Определите значение истинности следующего суждения « в <-> ~ в »: А. Истинно Б. Ложно В. Не определяемо...