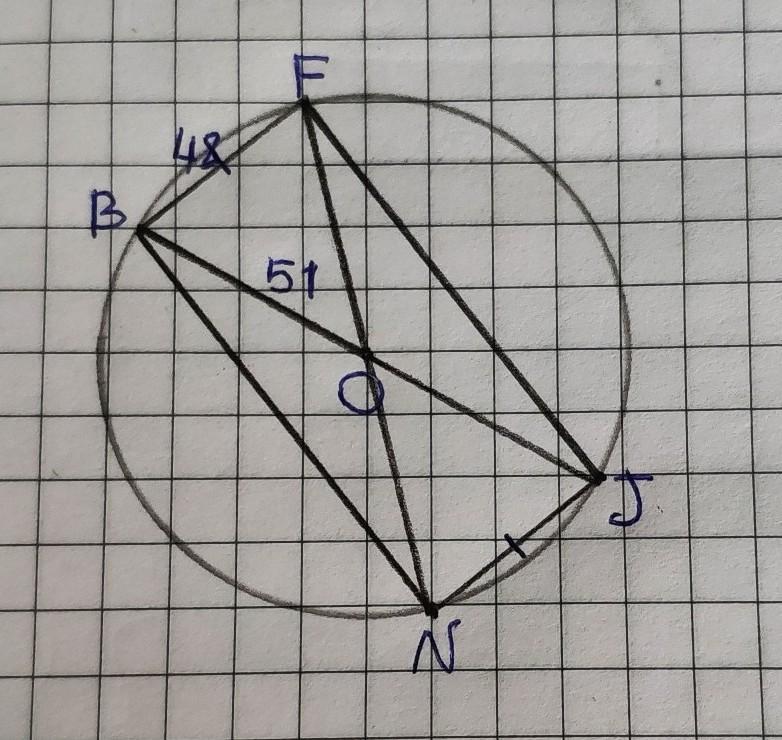
На окружности с центром в точке O по порядку отмечены 4 точки: B, F, J, N. Найди вторую сторону получившегося четырёхугольника, если BF∥NJ,BF=NJ, радиус этой окружности 51 см, а BF=48 см.​

Исходя из того, что точки расположены на окружности: полученный четырехугольник будет вписан в окружность.
Так как противоположные стороны четырехугольника BF и NJ равны и паралельны друг другу по условию, то четырехугольник BFJN – параллелограмм.
Параллелограмм, который можно вписать в окружность – прямоугольник.
Проведём диагонали BJ и FN. Точка пересечения диагоналей, вписанного в окружность прямоугольника, является центром этой окружности, следовательно каждая диагональ является диаметром.
Тогда BJ – диаметр окружности.
Диаметр окружности вдвое больше её радиуса, получим что BJ=51*2=102 см.
Рассмотрим ∆BJF.
Так как BFJN – прямоугольник, то угол BFJ=90°, а ∆BJF – прямоугольный.
BJ=102 см,
BF=48 см по условию.
По теореме Пифагора в ∆BJF:
BJ²=BF²+FJ²
102²=48²+FJ²
FJ²=10404–2304
FJ=√8100
FJ=90 см.
Получим что другая сторона четырехугольника равна 90 см. Так как данный четырехугольник – прямоугольник, то противоположная ей сторона равна так же 90 см.
Ответ: 90 см.