Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
16 февраля 2023 17:15
764
Доказать тождественную ложность следующих формул x&y&z&(x∨y∨z→¬w)&w
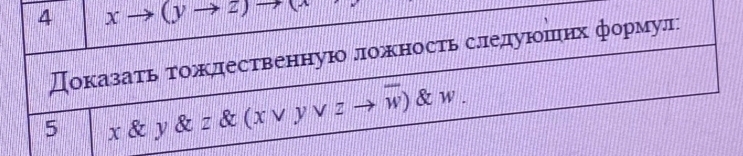
1
ответ
Для доказательства тождественной ложности данной формулы можно воспользоваться таблицей истинности или рассуждениями на естественном языке. Один из способов - построить контрпример, т.е. такое значение переменных, при котором формула принимает значение "ложь".
Для этого можно рассмотреть следующее значение переменных:
x = y = z = w = 1
Подставив значения переменных в исходную формулу, получим:
1 & 1 & 1 & (1 ∨ 1 ∨ 1 → ¬1) & 1
Вычислим выражение в скобках: 1 ∨ 1 ∨ 1 = 1, т.к. операция "или" возвращает значение "1", если хотя бы один из операндов равен "1".
Значит, выражение (1 ∨ 1 ∨ 1 → ¬1) равно ¬1, т.к. 1 ∨ 1 ∨ 1 = 1, а ¬1 = 0.
Тогда исходная формула примет вид:
1 & 1 & 1 & (¬1) & 1
Поскольку последнее выражение "1" (т.е. w = 1), то выражение в скобках должно быть "ложь" (т.е. ¬1), чтобы вся формула была "ложной". Однако, в нашем примере выражение в скобках равно "истина" (т.е. ¬1 = 0), а значит, исходная формула не является тождественно ложной.
Таким образом, мы не смогли найти контрпример для данной формулы и не смогли доказать ее тождественную ложность.
Для этого можно рассмотреть следующее значение переменных:
x = y = z = w = 1
Подставив значения переменных в исходную формулу, получим:
1 & 1 & 1 & (1 ∨ 1 ∨ 1 → ¬1) & 1
Вычислим выражение в скобках: 1 ∨ 1 ∨ 1 = 1, т.к. операция "или" возвращает значение "1", если хотя бы один из операндов равен "1".
Значит, выражение (1 ∨ 1 ∨ 1 → ¬1) равно ¬1, т.к. 1 ∨ 1 ∨ 1 = 1, а ¬1 = 0.
Тогда исходная формула примет вид:
1 & 1 & 1 & (¬1) & 1
Поскольку последнее выражение "1" (т.е. w = 1), то выражение в скобках должно быть "ложь" (т.е. ¬1), чтобы вся формула была "ложной". Однако, в нашем примере выражение в скобках равно "истина" (т.е. ¬1 = 0), а значит, исходная формула не является тождественно ложной.
Таким образом, мы не смогли найти контрпример для данной формулы и не смогли доказать ее тождественную ложность.
0
·
Хороший ответ
17 февраля 2023 05:07
Остались вопросы?
Еще вопросы по категории Математика
помогите решить пожалуйста...
К частному чисел 35 и 7 прибавить 18...
НАПИШИТЕ РЕАКЦИИ И НАБЛЮДЕНИЯ NaI+HCl=NaCl+HI Na2SO4+HCl≠ Na2SO4+2HCl=2NaCl+H2O+CO2↑ 2NaI+BaCl2=BaI2+2NaCl Na2SO4+BaCl2=Ba...
Решите уравнение: 1)3у=6 2)6у=3...
Әрбир гулзардын периметрин тап. Гул осируши арбир гулзардын коршагысы келди. Ол ушин узындыгы кандай коршау даярлау керек?...