Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
20 марта 2023 08:04
1074
найдите длину бокового ребра правильной треугольной призмы, если её сторона основания равна 2 ⁴√3, а объем 30 см³
2
ответа
В основании призмы - равносторонний треугольник, площадь находим по формуле через сторону такого треугольника.
Объем призмы= площадь основания * высоту.
Отсюда выражаем высоту
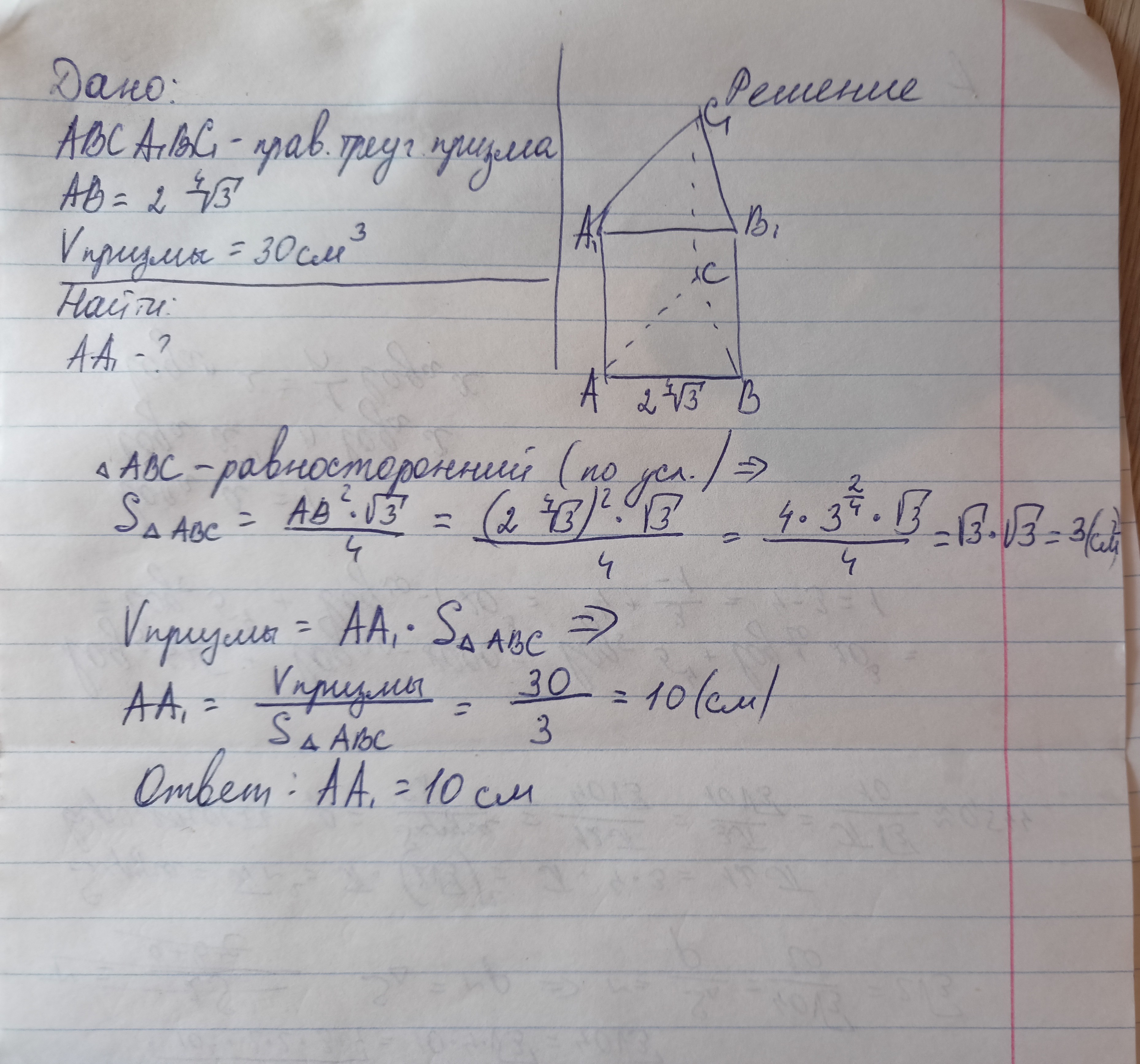
0
·
Хороший ответ
20 марта 2023 14:01
Для начала, найдем высоту правильной треугольной призмы. Обозначим ее через h.
Так как призма правильная, то высота боковой грани будет равна стороне основания, поделенной на 2.
h = (2 ⁴√3)/2 = 2 ³√3
Теперь можем найти площадь основания S.
S = (√3/4) * a², где a - сторона основания.
S = (√3/4) * (2 ⁴√3)² = 6√3
Объем призмы равен произведению площади основания на высоту.
V = S * h = 6√3 * 2 ³√3 = 12 * 3 = 36
Так как объем данной призмы равен 30 см³, то мы можем записать уравнение:
36a = 30
a = 5/6 ³√3
Таким образом, длина бокового ребра равна 5/6 ³√3.
Так как призма правильная, то высота боковой грани будет равна стороне основания, поделенной на 2.
h = (2 ⁴√3)/2 = 2 ³√3
Теперь можем найти площадь основания S.
S = (√3/4) * a², где a - сторона основания.
S = (√3/4) * (2 ⁴√3)² = 6√3
Объем призмы равен произведению площади основания на высоту.
V = S * h = 6√3 * 2 ³√3 = 12 * 3 = 36
Так как объем данной призмы равен 30 см³, то мы можем записать уравнение:
36a = 30
a = 5/6 ³√3
Таким образом, длина бокового ребра равна 5/6 ³√3.
0
20 марта 2023 08:04
Остались вопросы?
Еще вопросы по категории Математика
4÷8 деление с остатком...
Какие существительные в русском языке могут быть склоняемыми по разному?...
Найдите синус острого угла трапеции...
я прошу подробного объяснения темы: Деление десятичных Дробей Столбиком и не столбиком. Можете дать ссылку на любой сайт. Заранее спасибочки)...
Каждый час между двумя соседними кустами крапивы в ряду вырастает ещё два таких же. Сколько кустов нужно посадить изначально, чтобы через три часа общ...