и последняя задача на сегодня :площадь сечения куба плоскостью,проходящей через концы трех ребер ,выходящих из одной вершины,равна 18*корень 3.Просят найти ДЛИНУ РЕБРА КУБА

1 ответ

Посмотреть ответы

Megamozg

2200

Ответ:
Ребро куба равно 6 ед.
Объяснение:
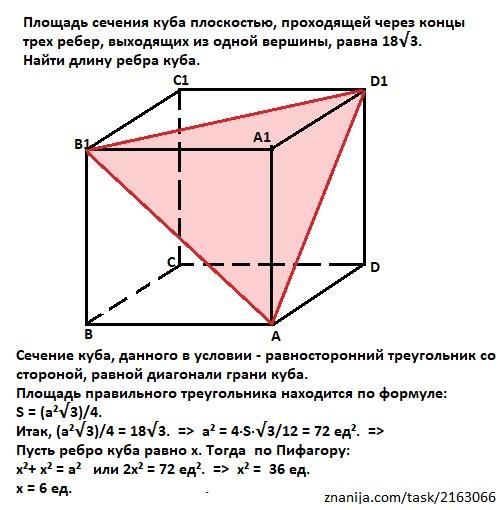
Сечение куба, данного в условии - равносторонний треугольник со стороной, равной диагонали грани куба.
Площадь правильного треугольника находится по формуле:
S = (a²√3)/4.
Итак, (a²√3)/4 = 18√3. => a² = 4·S·√3/12 = 72 ед². =>
Пусть ребро куба равно х. Тогда по Пифагору:
х²+ х² = а² или 2х² = 72 ед². => х² = 36 ед.
x = 6 ед.

Хороший ответ

3 апреля 2023 19:54

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

В прямоугольном треугольнике катет равен А гипотенуза С.Найдите косинус угла,противолежащего данному катету,если 1)А=10.С=12 2)А=3.С=5 3)А=1 С=2 Решит... Два угла четырёхугольника, вписанного в окружность, стягивают дуги в 140° и 130° соответственно. Найди наименьший из углов четырёхугольника.... 121 Отрезки АВ и CD пересекаются в середине О отрезка АВ, ∠OAD = ∠OBC. а) Докажите, что ΔСВО=ΔDAO; б) найдите ВС и СО, если CD=26 см, AD= 15 см.и 122... Диагональным сечением прямоугольного параллелепипеда, вписанного в шар, является квадрат. Найдите площадь этого диагонального сечения, если объем шара... Найти ортогональную проекцию точки (2;-3;1) на плоскость -x+3y-3z-5....