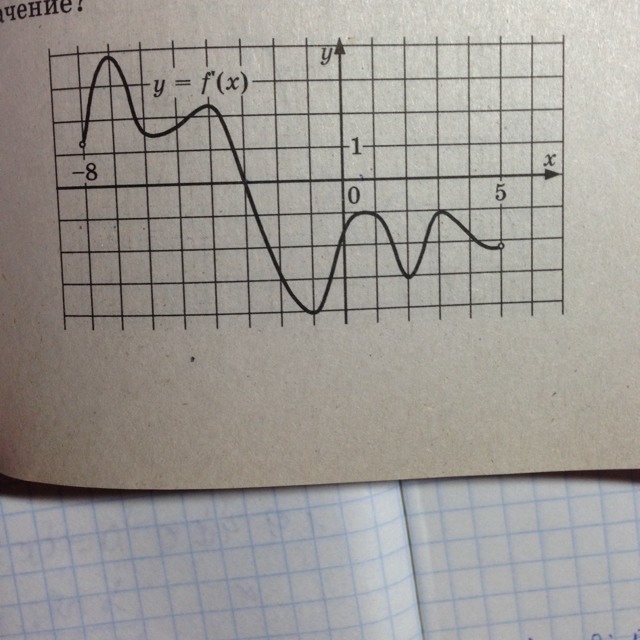
На рисунке изображен график производной функцииf(x), определенной на интервале (-8; 5). В какой точке отрезка [-3; 2] f(x) принимает наибольшее значение?

Постараюсь объяснить. Так как для производной существует правило: там, где она положительная ( здесь - выше оси ОХ) , функция растет, там , где производная отрицательная (ниже оси ОХ) - функция убывает. И еще. Точки, где производная равна нулю, то есть точки, где ее график пересекает ось ОХ, это критические точки, минимум или максимум, надо смотреть по графику, Вот здесь, например, в точке х=-3 - производная поменяла знак с плюса на минус, то есть была до этой точки выше , а после этой точки стала ниже оси ОХ, ТО есть точка х=-3 - это точка максимума, а раз эта точка принадлежит тому интервалу, где надо искать эту точку, то соответственно, именно здесь и будет наибольшее значение функции.