Большая высота параллелограмма равна 6. Найдите площадь параллелограмма, если биссектриса одного из его углов делит сторону параллелограмма на отрезки 10 и 14. Ответ должен получится 60, но у меня чего-то не выходит

1 ответ

Посмотреть ответы

Megamozg

2205

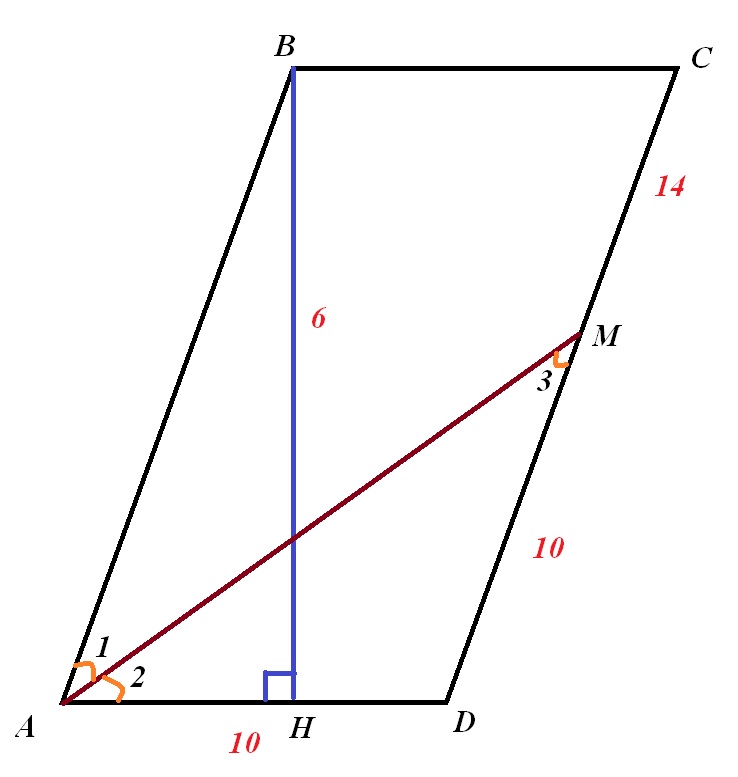
Чертеж во вложении.

В параллелограмме большая высота проходит перпендикулярно меньшей стороне.
Пусть АМ - биссектриса ∠А, которая пересекает сторону СD в точке М:
DМ=10, МС=14.

По определению биссектрисы ∠1 =∠2, еще ∠1 = ∠3(накрестлежащие), значит, ∠2 = ∠3.
Тогда ∆АМD - равнобедренный с основанием АМ. Поэтому АD=DМ=10.

Площадь параллелограмма S = BH*AD = 6*10=60.

Хороший ответ

3 апреля 2023 21:21

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

В правильной треугольной пирамиде сторона основания равна 4 корня из 3см,а плоский угол при вершине равен 90 градусов .Найдите высоту пирамиды... Яка градусна міра невідомого кута трапеції KMLN (ML || KN) на малюнку 86? А. 45° Б. 124° В. 56° Г. 135°... А(4;-2), B(8;0), C(6;4), D(2;2) дались четыре точки .Вид четырехугольника АВСD выявлятьA)квадрат В)ромб Г)трапеция Д)четырехугольник... в прямоугольном треугольнике гипотенуза равна 4√2 см А один из катетов равен 4 см , Найдите второй катет острые углы треугольника и его площадь... Решите, пожалуйста: Сторона равностороннего треугольника равна 20√3. Найдите радиус окружности, описанной около этого треугольника....