Найти острые углы прямоугольного треугольника, площадь которого равна 8 и гипотенуза равна 8.

1 ответ

Посмотреть ответы

DevAdmin

1720

Ответ:

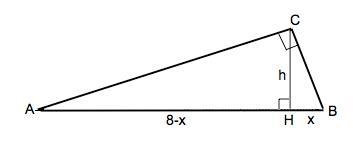
Объяснение: Назовем треугольник АВС; угол С=90°, АВ=8, Ѕ(АВС)=8, СН- высота.
—————
Одна из формул площади треугольника Ѕ=h•a/2, где h- высота, а - сторона, к которой высота проведена. Тогда 8=h•8/2, => h=2
Высота, которую провели из прямого угла на гипотенузу треугольника, равна среднему геометрическому проекций обоих катетов на эту гипотенузу ( т.е. отрезков, на которые она её делит).
Примем ВН=х. Тогда АН=8-х (см. рисунок).
СН²=ВН•АН
4=х•(8-х)⇒
х²-8х+4=0.
Решив квадратное уравнение, получим х₁=7,4641; х₂=0,5359
AH- больший отрезок, равен х₁=7,4641
tgA=CH:AH=2:7,4641=0,267949
∠ А=arctg 0,267949 ( по таблице Брадиса или калькулятору это угол 15°).
Из суммы острых углов прямоугольного тр-ка ∠ В=90°-15°=75°

Хороший ответ

3 апреля 2023 22:53

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

В прямоугольном треугольнике DCE с прямым углом C проведена биссектриса EF, причем FC = 13 см. Найдите расстояние от точки F до прямой DE.... Найдите площадь треугольника, вершины которого имеют координаты (0;0), (10;7), (7;10).... Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AP... Найдите синус,косинус и тангенс острых углов A и С прямоугольного треугольника ABC, если AC = 25см, AB = 7см.... Найдите длину отрезка АВ и координаты точки О-его середины, если А(-2;4) и В(4;10)....