Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
2 апреля 2023 00:58
1329
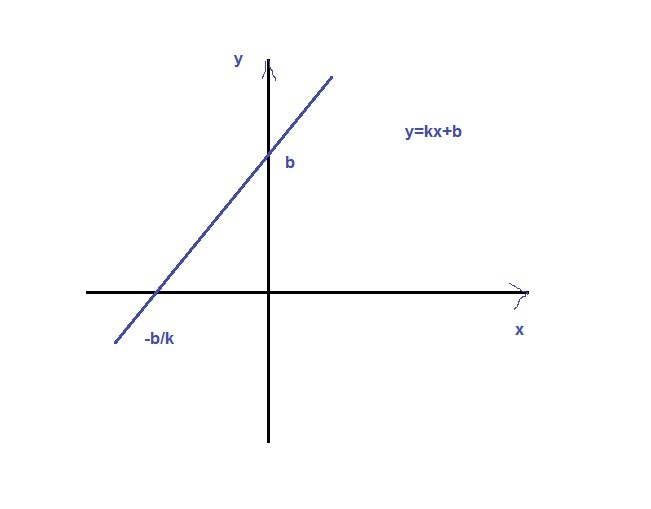
Часть графика линейной функции, расположенная во второй координатной четверти, вместе с осями координат образует треугольник. Во сколько раз изменится его площадь, если угловой коэффициент функции в 2 раза увеличить, а свободный член в два раза уменьшить?
1
ответ
Ответ:
треугольник прямоугольный с катетом =b
найдем другой катет при у=0 ; kx+b=0 x=-b/k длину катета берем по модулю = b/k
площадь исходного треугольника S=(1/2)b*b/k =(1/2)b²/k
площадь измененного треугольника S1=(1/2) ( b/2)²/(2k)=((1/2)b²/k)/8=S/8
площадь уменьшится в 8 раз
треугольник прямоугольный с катетом =b
найдем другой катет при у=0 ; kx+b=0 x=-b/k длину катета берем по модулю = b/k
площадь исходного треугольника S=(1/2)b*b/k =(1/2)b²/k
площадь измененного треугольника S1=(1/2) ( b/2)²/(2k)=((1/2)b²/k)/8=S/8
площадь уменьшится в 8 раз
0
·
Хороший ответ
4 апреля 2023 00:58
Остались вопросы?
Еще вопросы по категории Математика
Какое значение имеет число 1 в задании "10 х 6 1"?...
Пачка мороженого стоит 20 руб. Сколько денег было у Ани, если она купила 5 пачек мороженого и у неё осталось 11 руб?...
Чему равно количество молей в 1 ммоль?...
В июне 0,2 дней составили дождливые дни, ясные дни 1/2 дней, а остальные 9 дней были облачными.Сколько дней в и.не ?...
Как найти второй множитель если известен первый и произведение?плиииииииз помогите!!!!(ಥ_ಥ)...