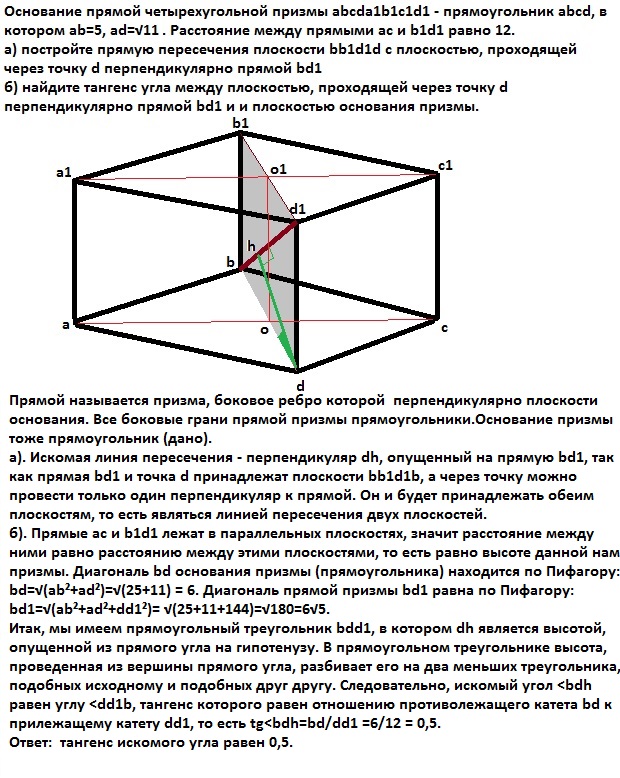
Основание прямой четырехугольной призмы abcda1b1c1d1 прямоугольник abcd, в котором ab=5, ad=11^1/2 (одиннадцать под корнем). Расстояние между прямыми ac и b1d1 равно 12.а) постройте прямую пересечения плоскости bb1d1d с плоскостью, проходящей через точку d перпендикулярно прямой bd1
б) найдите тангенс угла между плоскостью, проходящей через точку d перпендикулярно прямой bd1 и и плоскостью основания призмы.

Прямой называется призма, боковое ребро которой перпендикулярно плоскости основания. Все боковые грани прямой призмы прямоугольники.Основание призмы тоже прямоугольник (дано).
а). Искомая линия пересечения - перпендикуляр dh, опущенный на прямую bd1, так как прямая bd1 и точка d принадлежат плоскости bb1d1b, а через точку можно провести только один перпендикуляр к прямой. Он и будет принадлежать обеим плоскостям, то есть являться линией пересечения двух плоскостей.
б). Прямые ас и b1d1 лежат в параллельных плоскостях, значит расстояние между ними равно расстоянию между этими плоскостями, то есть равно высоте данной нам призмы. Диагональ bd основания призмы (прямоугольника) находится по Пифагору:
bd=√(ab²+ad²)=√(25+11) = 6. Диагональ прямой призмы bd1 равна по Пифагору:
bd1=√(ab²+ad²+dd1²)= √(25+11+144)=√180=6√5.
Итак, мы имеем прямоугольный треугольник bdd1, в котором dh является высотой, опущенной из прямого угла на гипотенузу. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два меньших треугольника, подобных исходному и подобных друг другу. Следовательно, искомый угол <bdh равен углу <dd1b, тангенс которого равен отношению противолежащего катета bd к прилежащему катету dd1, то есть tg<bdh=bd/dd1 =6/12 = 0,5.
Ответ: тангенс искомого угла равен 0,5.