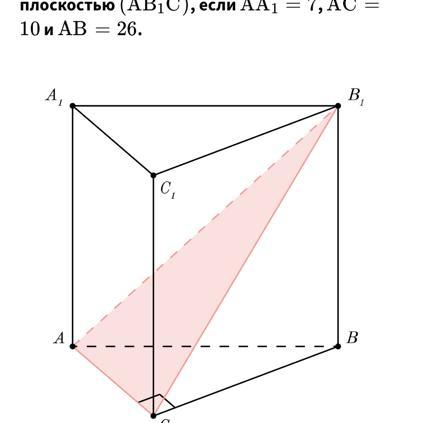
Найди площадь сечения прямой призмы плоскостью (AB1C), если AA1=7, AC=10 и AB=26

1 ответ

Посмотреть ответы

DevAdmin

1720

Ответ:
125 ед²

Решение:
∆АВС- прямоугольный треугольник
По теореме Пифагора
ВС=√(АВ²-АС²)=√(26²-10²)=
=√(676-100)=√576=24 ед.
ВВ1=АА1=7ед
∆В1ВС- прямоугольный треугольник
По теореме Пифагора
В1С=√(В1В²+ВС²)=√(7²+24²)=
=√(49+576)=√625=25 ед.
ВС перпендикулярно АС, → В1С перпендикулярно АС, Теорема о трех перпендикулярах.
∆АСВ1- прямоугольный треугольник
S(∆ACB1)=½*AC*CB1=10*25/2=
=125 ед²

Хороший ответ

4 апреля 2023 01:33

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B... Центр правильного треугольника АВС- точка О, его сторона равна 3. Отрезок ОМ-перпендикуляр к плоскости АВС, ОМ = 2. Найдите расстояние от точки М до в... Как найти площадь четверти круга радиусом 20 см, объсните плз!... Отрезок длины 29 см разделен на 5 равных частей. Найти расстояние между серединами крайних частей.... В треугольнике ABC угол С равен 90 градусов,А 30 градусов,СК=12 см-высота проведённая к гипотенузе АВ.Найдите расстояние от точки К до катета ВС...