Доказать, что NK || AC, MN || BC

1 ответ

Посмотреть ответы

Megamozg

2205

Ответ:
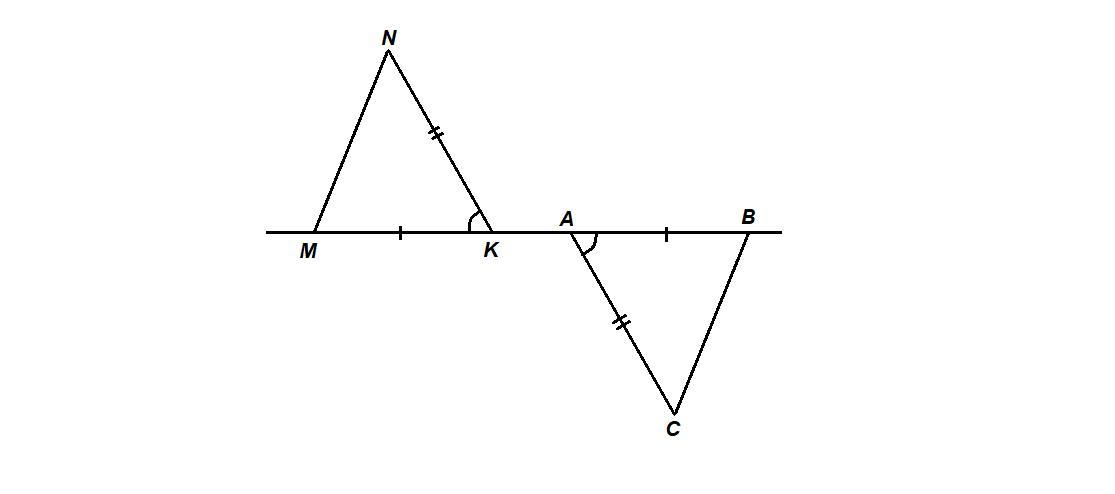
∠MKN = ∠CAB по условию,
эти углы - внутренние накрест лежащие при пересечении прямых NK и АС секущей ВМ, значит
NK ║ AC по признаку параллельности прямых.

По условию
МК = АВ, NK = АС, ∠NKM = ∠CAB, значит
ΔNKM = ΔCAB по двум сторонам и углу между ними.
Из равенства треугольников следует, что
∠NMK = ∠СВА,
эти углы - внутренние накрест лежащие при пересечении прямых MN и ВС секущей ВМ, значит
MN ║ ВС по признаку параллельности прямых.

Хороший ответ

4 апреля 2023 01:53

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Подобны ли треугольники ABC и DEF, если ∠A= 36°, ∠B = 34°, ∠E = 110°, ∠F=34°, АС=44см, АВ = 52см, BC=76см, DE = 15,6см, DF=22см, EF=13,2см?... На координатной плоскости изображена Парабола — график Квадратного трёхчлена y = ax²+ bx + c. Известны координаты точек А (-5; 0) и B (20; 0) — точек... Площадь полной поверхности конуса равна 108 π см², а его высота 6√3. Найдите угол наклона образующей конуса к плоскости его основания.... Нужно решить вместе с чертежом) Два внешних ушла треугольника равны 142 градуса и 82 градуса. Найдите углы, на которые высота треугольника делит его н... Периметр прямоугольника равен 62 см , а точка пересечения диагоналей удалена от одной из его сторон на 12 см.Найдите длину диагонали прямоугольника...