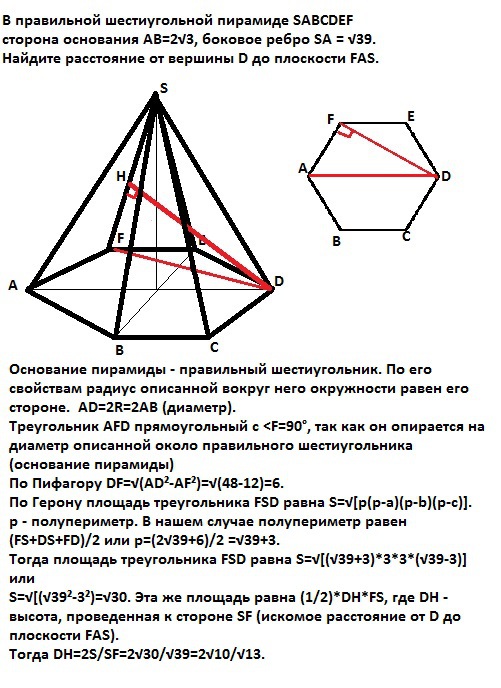
В правильной шестиугольной пирамиде SABCDEFсторона основания AB=2√3, боковое ребро SA = √39. Найдите расстояние от вершины D до плоскости FAS.

Основание пирамиды - правильный шестиугольник. По его свойствам радиус описанной вокруг него окружности равен его стороне. AD=2R=2AB (диаметр).
Треугольник АFD прямоугольный с <F=90°, так как он опирается на диаметр описанной около правильного шестиугольника (основание пирамиды) окружности.
AF=2√3(дано) AD=4√3.
По Пифагору DF=√(AD²-AF²)=√[(4√3)²-(2√3)²]=√(48-12)=6.
По Герону площадь треугольника FSD равна S=√[p(p-a)(p-b)(p-c)].
р - полупериметр. В нашем случае полупериметр равен (FS+DS+FD)/2 или р=(2√39+6)/2 =√39+3.
Тогда площадь треугольника FSD равна S=√[(√39+3)*3*3*(√39-3)] или
S=√[(√39²-3²)=√30. Эта же площадь равна (1/2)*DH*FS, где DH - высота, проведенная к стороне SF (искомое расстояние от D до плоскости FAS).
Тогда DH=2S/SF=2√30/√39=2√10/√13.