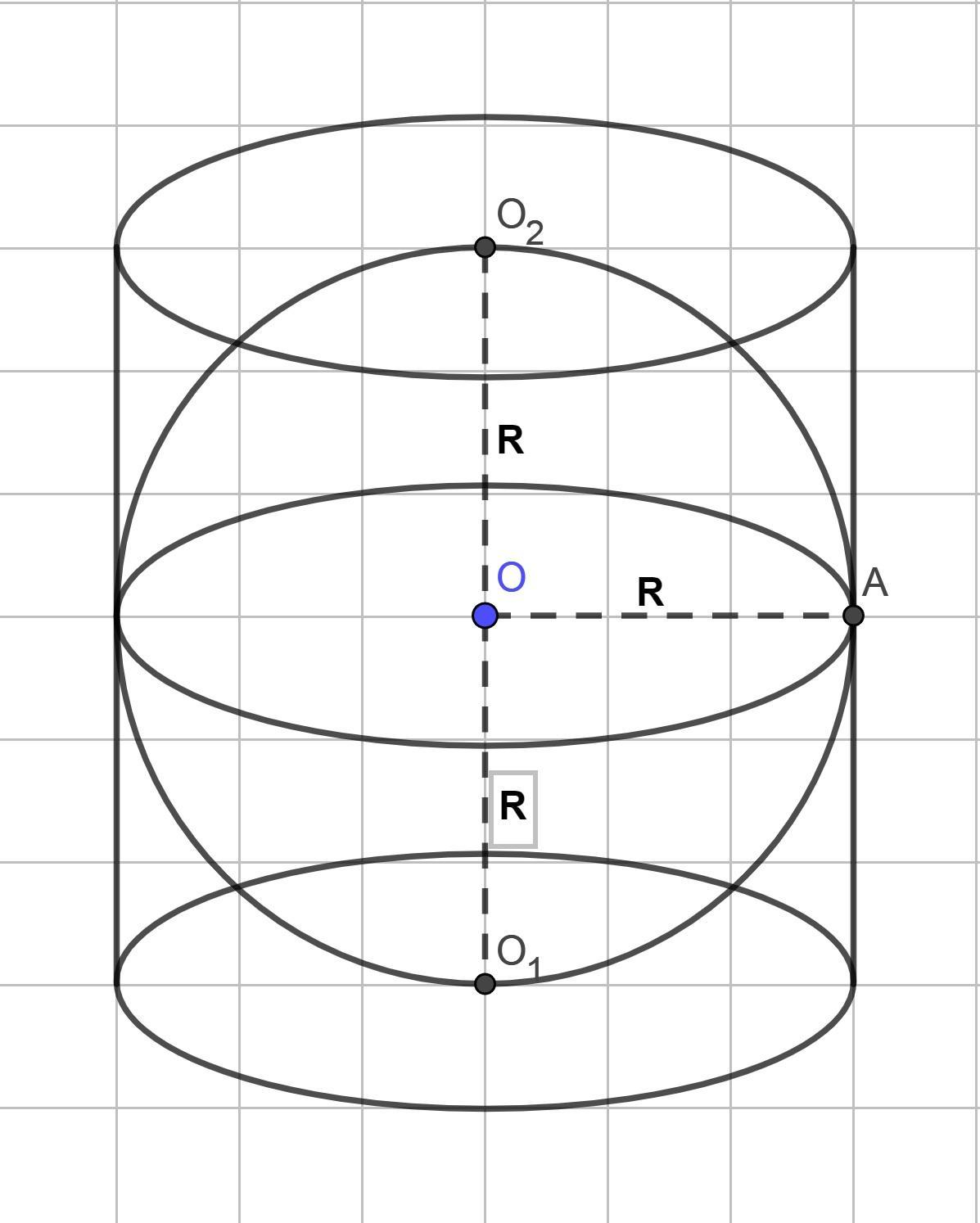
Шар вписан в цилиндр. Площадь поверхности шара равна 30. Найдите площадь полной поверхности цилиндра.

1 ответ

Посмотреть ответы

DevAdmin

1705

Sполн = 2πR² + 2πRL, где R - радиус основания, а L - образующая цилиндра
В нашем случае - осевое сечение цилиндра - квадрат (иначе не впишем в него шар) ⇒ L = 2R. Кроме того Rшара = R (см. рисунок)
Sполн = 2πR² + 4πR² = 6πR²
Sсферы = 4πR² = 30 ⇒ πR² = 30 ÷ 4 = 7,5
Sполн = 6 · 7,5 = 45

Хороший ответ

17 января 2023 06:06

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Что такое определение (в геометрии)?... Как начертить угол в 75 градусов с помощью циркуля и линейки без делений???... Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 3, а высота — 6.... В трапеции ABCD AB=CD высота BH делит основание на два отрезка меньший из которых равен 5.Найдите AD если ее средняя линия равна 9 см»... Докажите что противоположные грани параллепипеда паралельны и равны...