Решить неравенство:
Cos2x + cosx ≥0

1 ответ

Посмотреть ответы

DevAdmin

1720

$\cos2x + \cos x \geq 0$
$2\cos^2x-1 + \cos x \geq 0$
$2\cos^2x + \cos x-1 \geq 0$
Решим соответствующее квадратное уравнение:
$2\cos^2x + \cos x-1 =0$
$D=1^2-4\cdot2\cdot(-1)=9$
$\cos x=\dfrac{-1-3} =-1$
$\cos x=\dfrac{-1+3} =\dfrac$
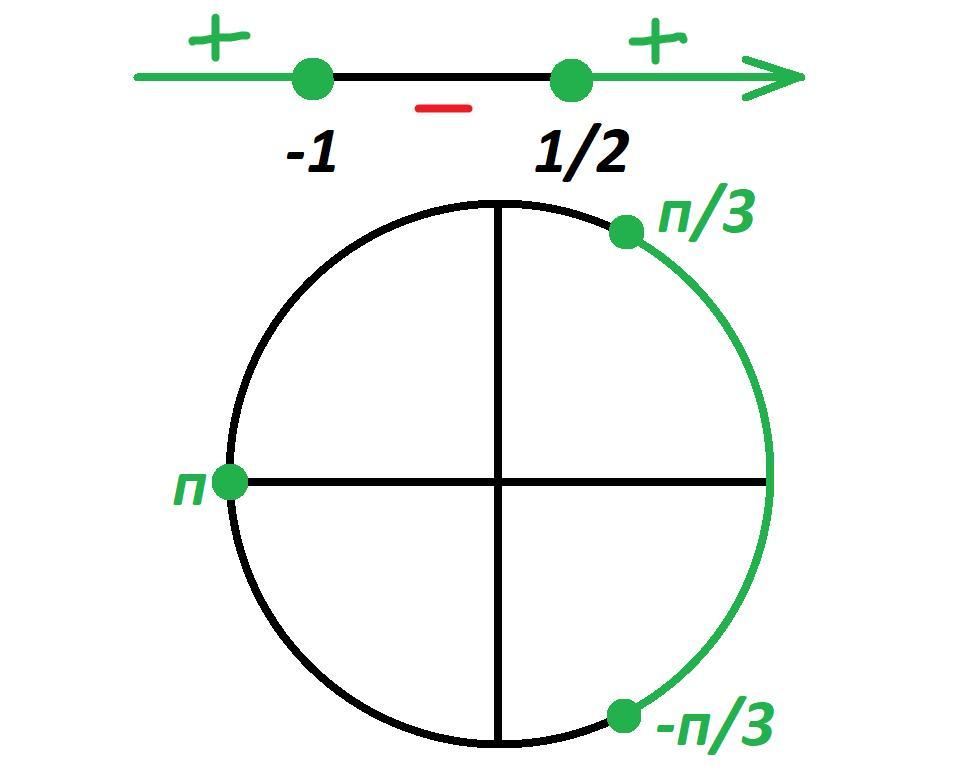
Дорешивая неравенство методом интервалов (картинка) получим:
$\cos x\in\left(-\infty;\ -1\right]\cup\left[\dfrac;\ +\infty\right)$
Учитывая, что косинус не принимает значения, по модулю превышающие 1, получим:
$\cos x\in\left\{-1\right\}\cup\left[\dfrac;\ 1\right]$
Рассматривая условие на числовой окружности (картинка), получим:
$x\in\{\pi+2\pi n\}\cup\left[-\dfrac{\pi}+2\pi n ;\ \dfrac{\pi}+2\pi n\right],\ n\in\mathbb$

Хороший ответ

4 апреля 2023 03:34

Остались вопросы?

Найти нужный

Еще вопросы по категории Алгебра

F(x)=1-x/1+x . Знайти f(x+1)... X²-11x+30=a(x-x1)(x-x2) найдите х1 и х2 помогите пожалуйста СОР... Катер прошел 80 км по течению реки и вернулся обратно, затратив на весь путь 9 часов. Найдите скорость течения реки, если скорость катера в стоячей во... Помогите,пожалуйста! Найдите наибольшее значение функции y = (21 - x)e^20-x на отрезке [19;21]. Очень часто с таким сталкиваюсь.Мы нашли производную и... Вычислите: а) sin 0 градусов + 2 cos 60градусов; б) tg 60 град * sin 60 град * ctg 30 град; в) 4 sin 90 град - 3 cos 180град; г) 3 сtg 90 град - 3 sin...

Решить неравенство: Cos2x + cosx ≥0

Решить неравенство:
Cos2x + cosx ≥0