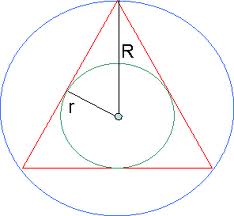
Помогите.. Радиус окружности,описанной около правильного треугольника,равен 16 см.Вычислите отношение площади данного треугольника к площади круга,вписанного в данный треугольник....

1 ответ

Посмотреть ответы

Megamozg

2205

! Известны следующие правила(теоремы, св-ва...): радиус окр-сти (круга) , описанной около прав. тр-ка в 2 раза больше радиуса вписанной окр-сти (круга) ;
сторона прав. тр-ка равна произведению радиуса опис. окр. на √3.
1) SΔ/ S кр= (a²·√3/4):(πr²)
Найдём а и r.
a= R·√3= 16√3 (cм); r =R/2= 16/2=8 (см), тогда

SΔ/ S кр= (a²·√3/4):(πr²)= ((16√3)²·√3/4):(π·8²)=( ¼·256·3√3)/ (64π)=3√3/π.
Ответ: в 3√3/π раз (приблизительно в 1,65 раз).

Хороший ответ

4 апреля 2023 05:25

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

АBCD параллелограмм.... Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 3 и 4, и боковым ребром, равным 5.... Две плоскости параллельны между собой. Из точки F. не лежащей ни в одной из этих плоскостей, ни между плоскостями, проведены две прямые. пересекающие... найти объем прямоугольного параллелепипеда, если стороны основания 2 и 3, а диагональ параллелепипеда √38... В чем заключается правило параллелограмма сложения двух неколлинеарных векторов...