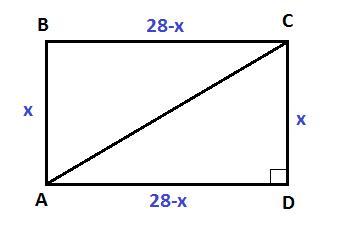
Периметр прямоугольника равен 56, а диагональ равна 27. Найдите площадь этого прямоугольника!

1 ответ

Посмотреть ответы

Megamozg

2205

Дано : прямоугольник ABCD, $P_=56;~AC=27$
Найти : $S_$
Решение :
$P_=2\cdot(AD+CD)=56\\~~~~~~~~~~~~~~~~~~~AD+CD=28~~\Rightarrow~~~\boldsymbol$
ΔACD - прямоугольный. Теорема Пифагора
$AD^2+CD^2=AC^2\\(28-CD)^2+CD^2=27^2\\28^2-2\cdot 28CD+CD^2+CD^2=729\\2CD^2-56CD+784-729=0\\\\2CD^2-56CD+55=0\\\\\dfrac D4=\bigg(\dfrac b2\bigg)^2-ac=\bigg(\dfrac 2\bigg)^2-2\cdot55=784-110=674\\\\CD=\dfrac{-\dfrac b2\pm\sqrt{\dfrac D4}}a=\dfrac}2=14\pm\sqrt$
$1)~CD=14+\sqrt\\~~~~~AD=28-\Big(14+\sqrt\Big)=14-\sqrt\\\\2)~CD=14-\sqrt\\~~~~~AD=28-\Big(14-\sqrt\Big)=14+\sqrt\\\\$
$S_=AD\cdot CD=\\\\=\Big(14-\sqrt\Big)\Big(14-\sqrt\Big)=\\\\=14^2-\sqrt^2=196-168,5=27,5$
Ответ : 27,5

Хороший ответ

4 апреля 2023 06:27

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Прямая МК разбивает плоскость на две полуплоскости. Из точек М и К в разные полуплоскости проведены равные отрезки МА и КВ, причем угол АМК = углу ВКМ... отрезки KL и MN пересекаются в точке O которая является серединой отрезка KL известно что угол MKL = углуNLK. найдите отношение MO: ON... Дайте только ответ ... Известно, что VN||AC , AC= 12 м, VN= 6 м, AV= 4,2 м. Вычисли стороны VB и AB .... Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равна 5,5. Найдите объем параллелепипеда.... Через вершину квадрата ABCD проведена прямая ВМ, перпендикулярная его плоскости. Докажите, что: 1) прямая AD перпендикулярна плоскости прямых АВ и ВМ;...