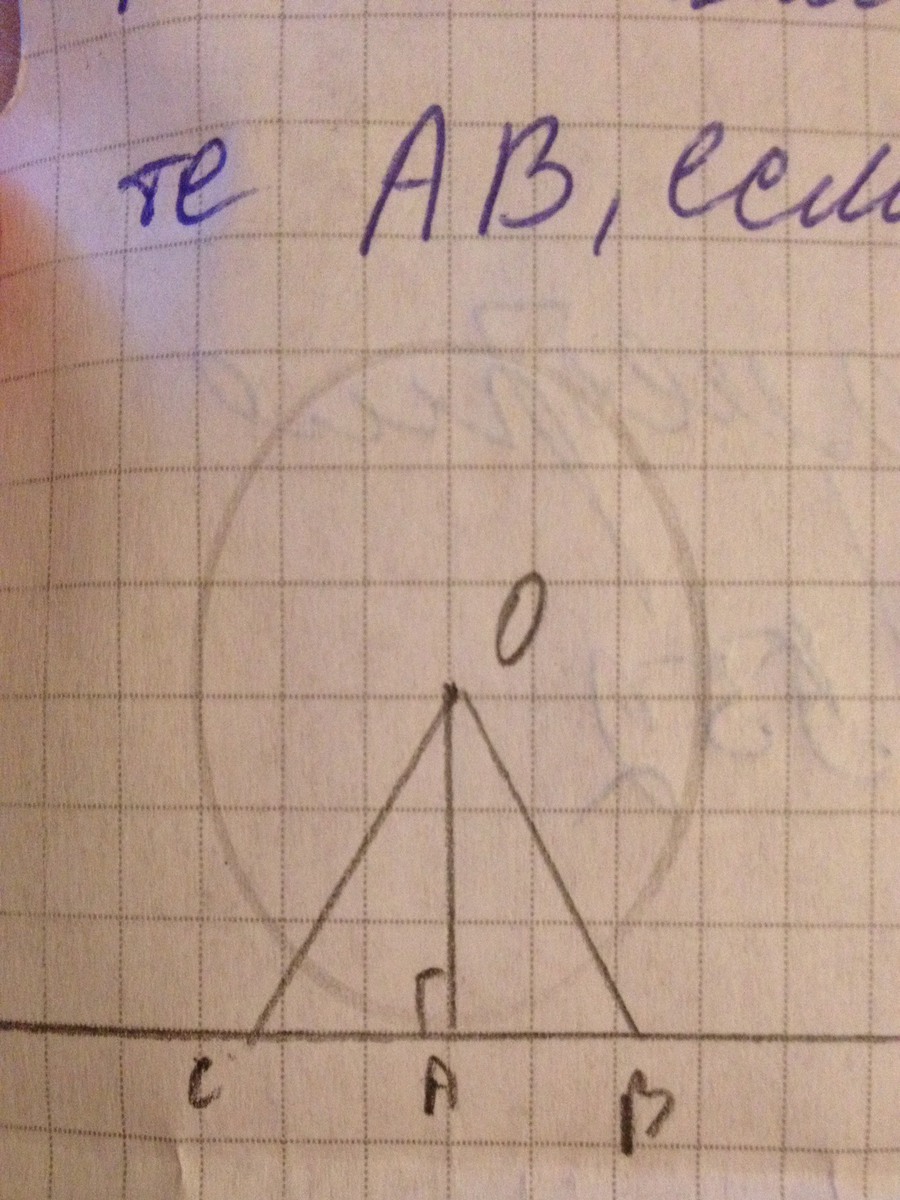
Прямая касается окружности с центром О в точке А. На касательной по разные стороны от точки А отметили точки В и С такие, что ОВ=ОС. Найдите АВ,если АС=6см

1 ответ

Посмотреть ответы

Megamozg

2205

ОА⊥СВ, так как радиус, проведенный в точку касания перпендикулярен касательной.
ΔВОС равнобедренный, так как ОВ = ОС по условию, ОА - его высота, а следовательно и медиана:
АВ = АС = 6 см.

Хороший ответ

4 апреля 2023 10:57

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Четырёхугольник ABCD вписан в окружность. Угол ABC равен 80°, угол CAD равен 54°. Найдите угол ABD. Ответ дайте в градусах.... В треугольнике ABC AB=6 см, BC=8 см.Через середину стороны AC проведены прямые, параллельные сторонам AB и BC.Найдите периметр образовавшегося четырёх... проведите прямую, обозначьте ее буквой m. Отметьте точки А и В, лежащие на этой прямой ,и точки С, D,E,не лежащие на ней .... Сформулируйте и докажите теорему о вычислении площади параллелограмма... 2. Пусть d - расстояние от центра окружности радиуса r до прямой р. Каково взаимное расположение прямой р и окружности, если: a) r = 10 дм, d = 10 дм;...