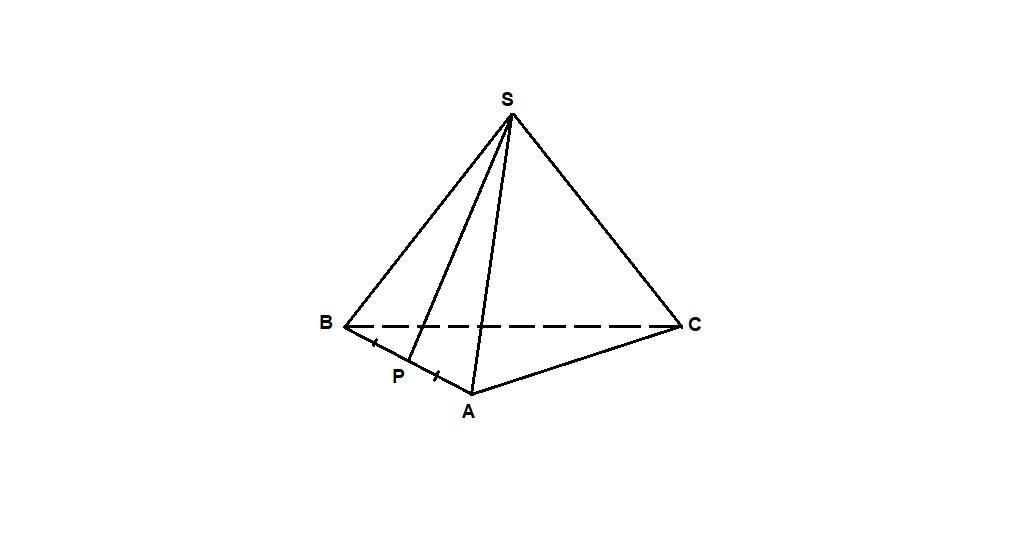
В правильной треугольной пирамиде SABC точка P - середина ребра AB, S-вершина . Известно, что SP=4,а площадь боковой поверхности равна 24. Найдите длину отрезка BC.

Ответ:
4
Пошаговое объяснение:
Пирамида правильная, значит основание - правильный треугольник, а боковые грани - равные равнобедренные треугольники.
Площадь боковой поверхности вычисляется по формуле:

где Р - периметр основания,
l - апофема (высота боковой грани)
Тогда
Р - середина АВ, значит SP - медиана и высота ΔSAB, т.е.
SP = 4 - апофема.

BC = P / 3 = 12 / 3 = 4