площадь поверхности правильного тетраэдра 12 корней из 3.Найдите площадь поверхности конуса ,вписанного в этот тетраэдр

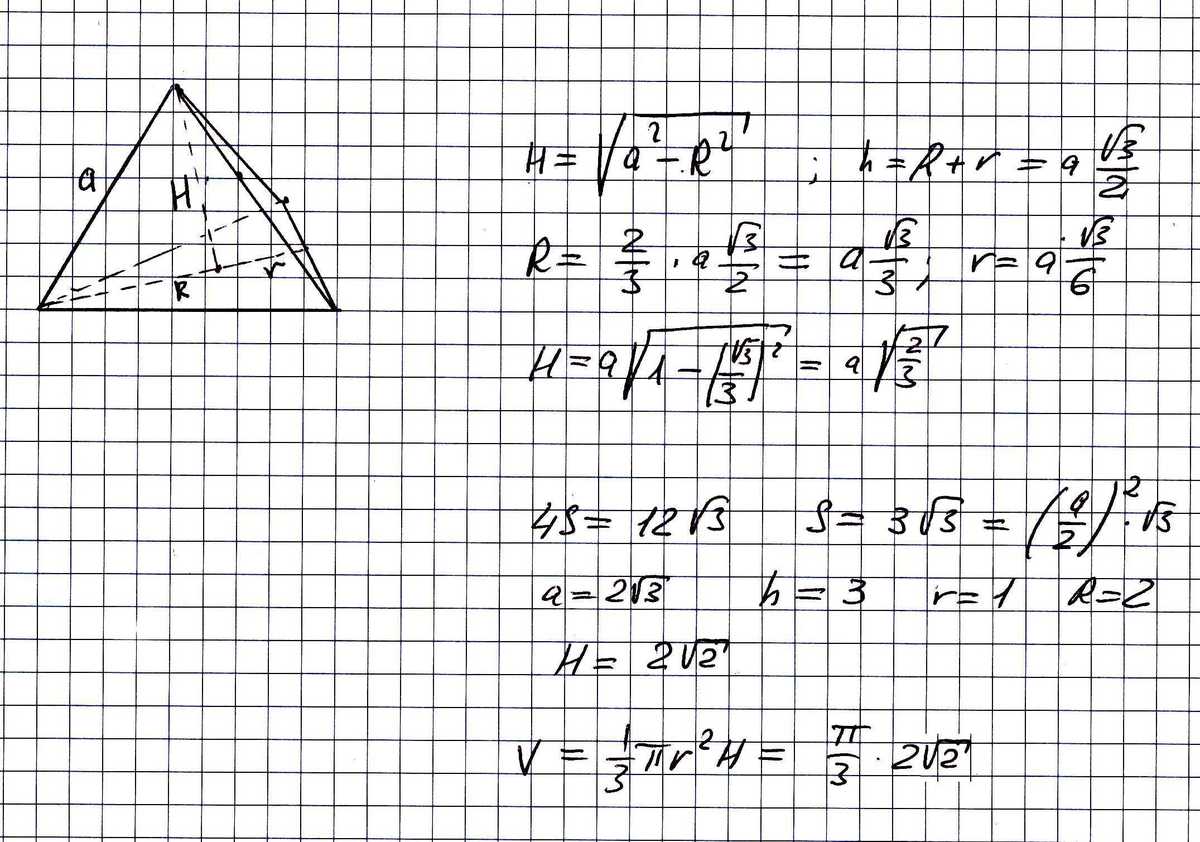
на рисунке четреж и "сухое" решение.
Я считаю, что все 4 грани одинаковые равносторонние треугольники со стороно a, то есть это самый что ни на есть тетраэдр. :)
H - высота пирамиды,она же высота конуса. h - высота любой боковой грани.
Вписанный конус будет иметь в основании круг, вписанный в треугольник. Его радиус равен трети высоты h.
h = a*корень(3)/2;
Поэтому S = 12*корень(3)/4 = (a/2)^2*корень(3); a = 2*корень(3); h = 3, r = 1; R = 2.
H = корень(a^2 - R^2) = 2*корень(2);
Остается вычислить объем конуса.
V = (1/3)*pi*r^2*H = 2*pi*корень(2)/3

Ой... надо было площадь поверхности искать... :((( пардон, спешил...
S основания = pi^r^2 = pi.
Образующая равна апофеме, то есть h = 3 :). Пдощадь боковой поверхности
Sb = pi*h*r = 3*pi; (прикольно, пропорция та же... впрочем можно было бы сразу понять - угол наклона боковой поверхности тот же - примечание для супергеометров :)))
Полная площадь 4*pi.