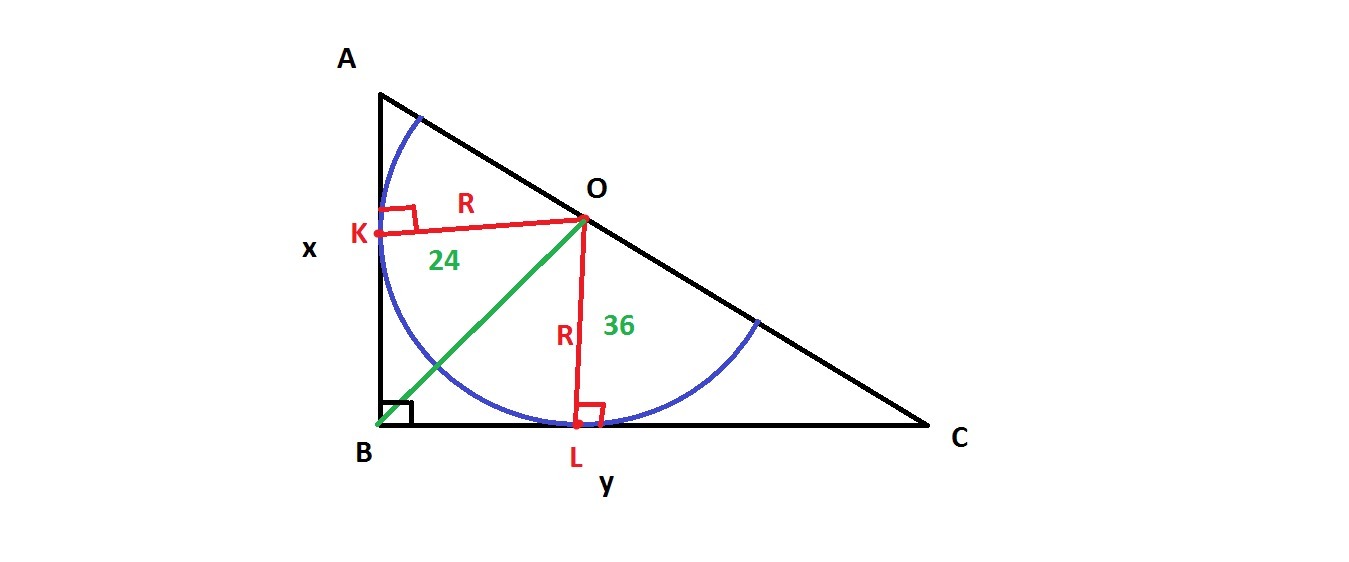
Полуокружность,центр O которого лежит на гипотенузе AC прямоугольного треугольника ABC, касается катетов. Найдите площадь квадрата со стороной AC, если отрезок BO разбивает площадь треугольника на части 24 см^2 и 36 см^2.

2 ответа

Посмотреть ответы

Megamozg

2205

Площадь ΔАВС=24+36=60

Пусть АВ=х, а ВС=у
Проведем радиусы в точки касания К и L, то есть ОК=OL=R
По теореме радиус, проведенный в точку касания, перпендикулярен самой касательной. То есть ∠АКО=∠ВLO=90°

$S_= \fracah= \frac *BC*OL=\frac*y*R \\ \\ S_=\frac*AB*OK=\frac*x*R$

по условию площадь ΔАОВ=24 и площадь ΔВОС=36.

$\left \{ {{ \frac*y*R=36} \atop {\frac*x*R=24}} \right. \ \ =\ \textgreater \ \ \ \left \{ { \atop } \right.$

поделим первое уравнение на второе:

$\frac= \frac \ \ =\ \textgreater \ \ \ \frac =1.5$

$S_= \frac *AB*BC=\frac *x*y$

зная, что площадь ΔАВС=60, запишем еще одну систему:

$\left \{ {{\frac *x*y=60} \atop {\frac =1.5}} \right. \ \ =\ \textgreater \ \ \ \left \{ { \atop y=1.5x}} \right. \\ \\ x*1.5x=120 \\ \\ 1.5x^2=120 \\ \\ x^2=120/1.5=80 \\ \\ x=4 \sqrt \\ \\ y=1.5x=1.5*4 \sqrt =6 \sqrt$

Площадь квадрата со стороной АС = АС²

АС² найдем по теореме Пифагора из ΔАВС:

$AC^2=AB^2+BC^2=x^2+y^2=(4 \sqrt )^2+(6 \sqrt )^2=80+180=260 \\ \\$

ОТВЕТ: 260 см²

Хороший ответ

4 апреля 2023 08:10

Megamozg

2205

Радиус окружности перпендикулярен касательной к ней.

Значит высоты обоих треугольников будут равны.

AB*r/2=24
BC*r/2=36

Приравняем r/2.

r/2=24/AB=36/BC

BC=1.5AB

Площадь прямоугольного треугольника равна произведению катетов делённому на 2, следовательно:

24+36=BC*AB/2
60=1.5AB^2/2
120=1.5AB^2
AB^2=80

BC^2=2.25AB^2
BC^2=180

По т. Пифагора:

AC^2=AB^2+BC^2=80+180=260

Площадь квадрата равна его стороне в квадрате, то есть:

S=AC^2=260

Ответ: 260.

4 апреля 2023 08:10

Остались вопросы?

Найти нужный

Еще вопросы по категории Математика

В США альтернативные издержки производства 1 кг зерна составляют 50 велосипедов. В Китае альтернативные издержки производства 1 велосипеда составляют... Как выполнить задание '1 десятая'?... Сколько будет 0+(-4)?... Разложите на простые множители число:Сегодня 27,56,625 820, 2772 702 1224... Какое количество дециметров соответствует 1 метру?...