Из точки D, которая лежит вне плоскости α, проведены к этой плоскости наклонные DK и DB, образующие с ней углы 45° и 60° соответственно. Найдите длину проекции наклонной DK на плоскость α, если DB = 10 корней из 3

1 ответ

Посмотреть ответы

Megamozg

2205

Ответ:
15 ед.
Объяснение:
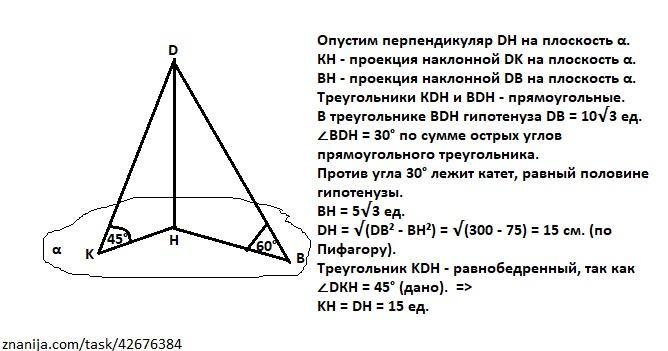
Опустим перпендикуляр DH на плоскость α.
КН - проекция наклонной DK на плоскость α.
ВН - проекция наклонной DВ на плоскость α.
Треугольники КDH и BDH - прямоугольные.
В треугольнике BDH гипотенуза DB = 10√3 ед.
∠BDH = 30° по сумме острых углов прямоугольного треугольника.
Против угла 30° лежит катет, равный половине гипотенузы.
ВН = 5√3 ед.
DH = √(DB² - BH²) = √(300 - 75) = 15 см. (по Пифагору).
Треугольник KDH - равнобедренный, так как
∠DКH = 45° (дано). =>
KH = DH = 15 ед.

Хороший ответ

4 апреля 2023 10:22

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Найдите длину неизвестной стороны треугольника NPK, если NP=3см, NK= 2 корня из 2 см и угол N=135 градусов... Около окружности описана трапеция, периметр которой равен 40. Найдите ее среднюю линию.... Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает сто... Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 3 и 4, и боковым ребром, равным 5.... СРОЧНО ПОЖАЛУЙСТА ПОМОГИТЕ! Стороны параллелограмма равны 6 см и 24 см, а высота, проведённая к большей стороне, равна 3,6 см. Вычисли высоту, провед...