Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
2 апреля 2023 12:10
973
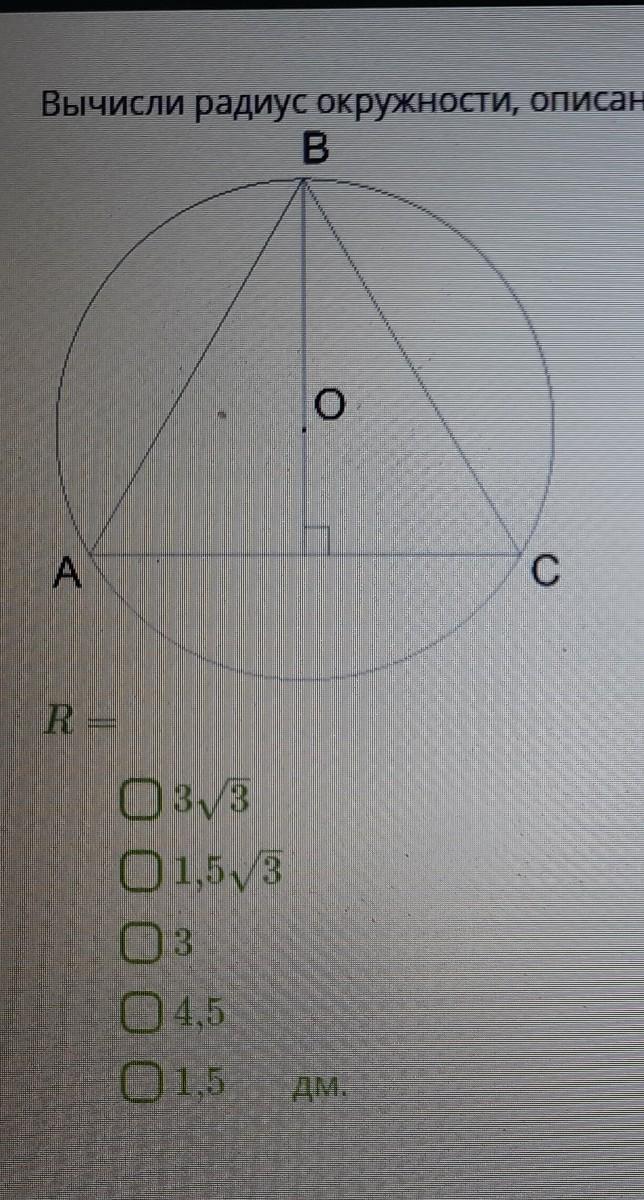
Вычисли радиус окружности , описанной около равностороннего треугольника, если его сторона равна 3 корня из 3 дм
1
ответ
Ответ:
3 дм
Объяснение:
Треугольник равносторонний, значит ВН - высота и медиана.
 дм
дм
Из прямоугольного треугольника АВН по теореме Пифагора:

 дм
дм
 , так как О - центр правильного треугольника (точка пересечения медиан).
, так как О - центр правильного треугольника (точка пересечения медиан).
Радиус описанной окружности:
 дм
дм
____________________
Лучше запомнить формулу радиуса окружности, описанной около равностороннего треугольника со стороной а:

 дм
дм
 дм
дм
3 дм
Объяснение:
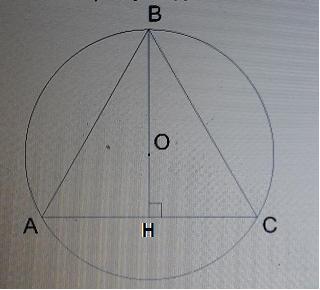
Треугольник равносторонний, значит ВН - высота и медиана.
Из прямоугольного треугольника АВН по теореме Пифагора:
Радиус описанной окружности:
____________________
Лучше запомнить формулу радиуса окружности, описанной около равностороннего треугольника со стороной а:
1
·
Хороший ответ
4 апреля 2023 12:10
Остались вопросы?
Еще вопросы по категории Геометрия
Что такое смежный угол? (если можно,с картинкой)...
Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y=x-17 или совпадает с ней. Подробней на картинке....
Докажите, что биссектрисы треугольника пересекаются в одной точке....
Решите пожалуйста! В треугольнике 2 угла равны 43 и 88 градусов. Найдите его 3 угол...
ДАЮ 10 БАЛЛОВ!!! покажите, что прямая содержащая середины двух параллельных хорд, проходит через центр окружности...