Хорда нижнего основания цилиндра удалена от центра нижнего основания на 2 корня из трех и отсекает от окружности основания дугу в 60 градусов.Отрезок, соединяющий центр верхнего основания с одним из концов данной хорды, образует с осью цилиндра угол 45 градусов. Найдите площадь осевого сечения цилиндра.

1 ответ

Посмотреть ответы

Megamozg

2180

Площадь осевого сечения цилиндра равна произведению диаметра его основания на высоту.
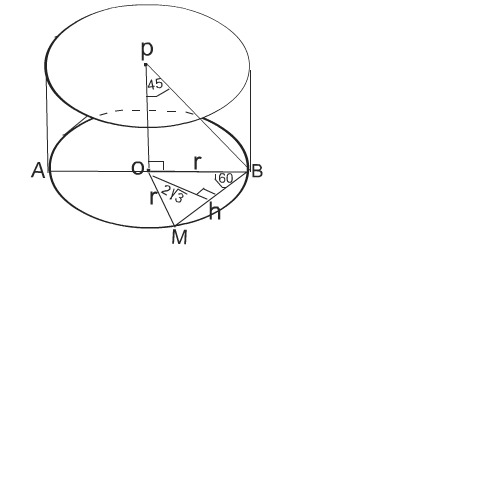
Поскольку отрезок, соединяющий центр верхнего основания с одним из концов данной хорды образует с осью цилиндра угол 45 градусов, высота цилиндра равна его радиусу r ( см.рисунок).
Площадь осевого сечения даного цилиндра равна
S=r·2r= 2r²
Чтобы найти радиус основания цилиндра, рассмотрим Δ МОВ. Этот треугольник - равносторонний, так как образован хордой и двумя радиусами, угол между которыми равен 60 °.
Высота этог трегольника 2√3, по формуле высоты равностороннего треугольника найдем сторону его а
(а√3):2=2√3, где а=r - сторона треугольника МОВ.
а√3 =2*2√3
а=4
Итак, радиус окружности основания равен 4 см, диаметр 8 см, высота цилиндра 4 см.
S осевого сечения=2r²=32 см²

Хороший ответ

4 апреля 2023 13:15

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Выведите формулу для вычисления расстояния между двумя точками по их координатам.... расстояния от вершины параллелограмма до точки пересечения диагоналей равны 8см и 13см. Какова длина каждой диагонали? В ответ пишем величины без... Точка H является основанием высоты BH , проведенной из вершины прямого угла B прямоугольного треугольника ABC . Окружность с диаметром BH пересекает с... Реши уравнение cosx=1: x=±arccos (вставить недостающую деталь) +2πk,k∈Z... в прямом параллелепипеде ABCDA1B1C1D1 AD=2,CD=3,уголADC=120, A1C=корень из 35. найдите площади боковой и полной поверхности параллелепипеда. если можн...