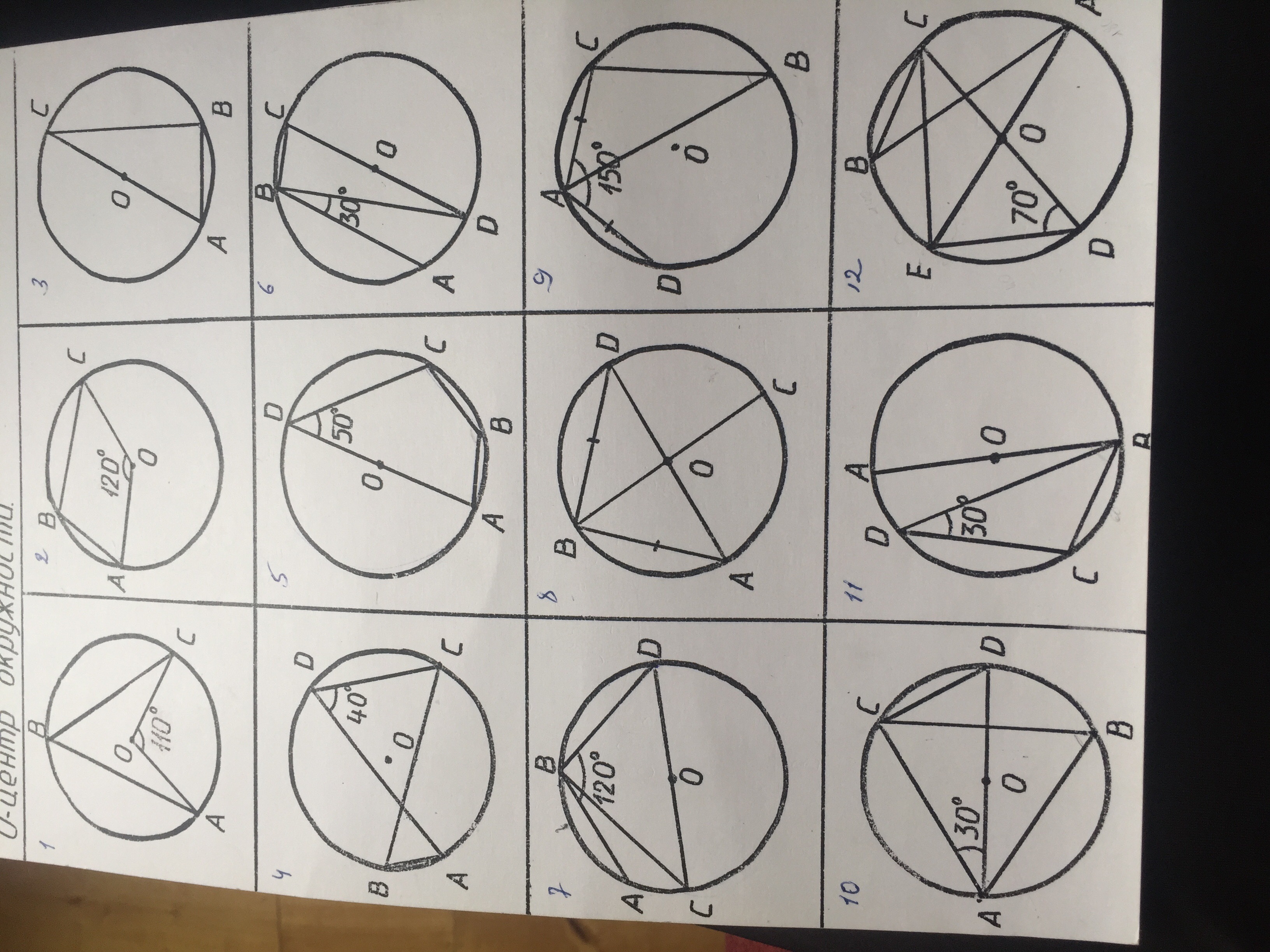
Найти градусную меру угла ABC
Пожалуйста!
90 баллов !очень нужно !

1. ∠ABC - вписанный, ∠AOC - центральный. Они опираются на одну и ту же дугу ⇒ ∠AOC = 2∠ABC, откуда ∠ABC = 110°/2 = 55°

2. Градусная мера дуги ABC = 120°. Градусная мера дуги AC = 360° - 120° = 240°. ∠ABC вписан, опирается на AC ⇒ ∠ABC = 240°/2 = 120°

3. ∠ABC опираются на диаметр ⇒ ∠ABC = 90°

4. Вписанные углы ABC и ADC опираются на одну и ту же дугу ⇒ ∠ABC = ∠ADC = 40°

5. Градусная мера дуги ABC = 50°*2 = 100°. Градусная мера дуги ADC = 360° - 100° = 260°. ∠ABC вписан, опирается на ADC ⇒ ∠ABC = 260°/2 = 130°

6. ∠CBD опираются на диаметр ⇒ ∠СBD = 90°. ∠ABC = ∠СBD + ∠DBA = 90° + 30° = 120°

7. ∠CBD опираются на диаметр ⇒ ∠СBD = 90°. ∠ABC = ∠DBA - ∠СBD = 120° - 90° = 30°

8. ∠ABD опираются на диаметр ⇒ ∠ABD = 90°. BO - медиана, так как DO = OA = R. ΔABC р/б, так как AB = BD ⇒ BO не только медиана, но и биссектриса ⇒ ∠ABC = 1/2∠ABD = 45°

9. Градусная мера дуги DBC = 150°*2 = 300°. Градусная мера дуги CAD = 360° - 300° = 60°. Градусные меры дуг AC и AD равны, так как AC = AD ⇒ градусная мера дуги AC = 60°/2 = 30°. ∠ABC вписан, опирается на AC ⇒ ∠ABC = 30°/2 = 15°

10. Градусная мера дуги DC = 30°*2 = 60°. Дугу ACD стягивает диаметр ⇒ градусная мера дуги ACD = 180°. Градусная мера дуги AC = 180° - 60° = 120°. ∠ABC вписан, опирается на AC ⇒ ∠ABC = 120°/2 = 60°

11. Градусная мера дуги BC = 30°*2 = 60°. Дугу ADCB стягивает диаметр ⇒ градусная мера дуги ADCB = 180°. Градусная мера дуги AC = 180° - 60° = 120°. ∠ABC вписан, опирается на AC ⇒ ∠ABC = 120°/2 = 60°

12. Градусная мера дуги EBC = 70°*2 = 140°. Дугу ACBE стягивает диаметр ⇒ градусная мера дуги ACBE = 180°. Градусная мера дуги AC = 180° - 140° = 40°. ∠ABC вписан, опирается на AC ⇒ ∠ABC = 40°/2 = 20°