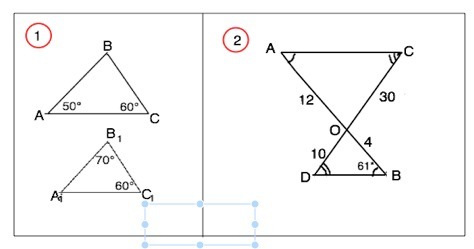
8 класс Самостоятельная работа Вариант 2Тема: «Признаки подобия треугольников»
1) Дано: А=50˚,
С=60˚, С1=60˚,
В1=70˚.
Доказать:
ΔАВС ΔА1В1С1

2) Дано: АО=12, ВО=4,
СО=30, DО=10, DВО=61˚, АСIIDB
Найти: САО и отношение площадей ΔАОС и ΔВОD.

1 ответ

Посмотреть ответы

DevAdmin

1720

1) Сумма углов треугольника 180°. В ∆ АВС угол В=180°-50°-60°=70°. В ∆ А1В1С1 угол А1=180°-708-608=50°. Треугольники АВС и А1В1С1 подобны по равенству всех углов.
2) По условию АС║BD, АВ и СD - секущие. Образовавшиеся при пересечении секущими параллельных прямых накрестлежащие углы равны. ⇒ ∠СAО=∠DBO=61°. Треугольники АОС и BOD подобны по равенству накрестлежащих углов, а стороны, содержащие вертикальные углы при О - пропорциональны. k=АО:ВО=12:4=3, k=СО:DO=30:10=3. Отношение площадей подобных фигур равно квадрату коэффициента их подобия. S(AOC):S(BOD)=k²=3²=9

Хороший ответ

5 апреля 2023 09:26

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

В треугольнике abc ab=bc=10, высота ah=5. Найдите угол c.... Помогите.. Радиус окружности,описанной около правильного треугольника,равен 16 см.Вычислите отношение площади данного треугольника к площади круга,впи... в прямоугольном треугольнике ABC угол С= 90 градусов,угол А=30 градусов, ВС= 12 в квадратном корне 2.Найдите гипотенузу Срочно,заранее спасибо... Геометрия 7 кл задача. Треугольники ADE и MLK - прямоугольные, у которых гипотенузы AD и ML равны. Известно, что угол A = 32 гр. угол L = 58 гр.Укажит... Даны компланарные векторы ~a, ~b и ~c, причем a = 3, b = 2, c = 5, ( c~a,~b) = 60◦ и ( ~cb,~c) = 60◦ . Построить вектор ~u = ~a + ~b − ~c и вычислить...