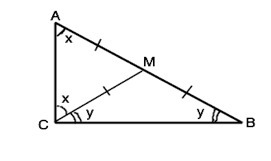
Докажите что , если медиана треугольника равна половине стороны , к которой она проведена , то треугольник прямоугольный.

1 ответ

Посмотреть ответы

Megamozg

2205

Пусть в ∆ АВС отрезок СМ - медиана и по условию СМ=АМ=ВМ. Тогда ∆ АМС и ∆ ВМС - равнобедренные с равными углами при основаниях. Примем ∠МАС=∠МСА=х, и ∠МСВ=МВС =у
Сумма углов треугольника 180° ⇒ 2х+2у=180° ⇒ х+у=90°. Тогда ∠АСВ=х+у=90°. ⇒ ∆ АВС - прямоугольный. Доказано.

Хороший ответ

4 апреля 2023 14:37

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

В треугольнике ABC угол С равен 90 градусов,А 30 градусов,СК=12 см-высота проведённая к гипотенузе АВ.Найдите расстояние от точки К до катета ВС... На рисунке 34 угол 1= углу 2. Докажите что AB=BC... Точка К находится на расстоянии 6см. от плоскости,наклонные КА и КВ образуют с плоскостью углы 45 и 30 градусов, угол между проекциями наклонных 135 г... Решите пожалуйста! В треугольнике 2 угла равны 43 и 88 градусов. Найдите его 3 угол... В четырехугольнике ABCD стороны AB и CD параллельны и равны, а его периметр равен 32 см. Найдите сумму длин AD и AB....