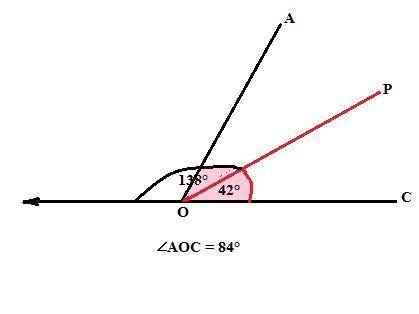
Угол между биссектрисой угла АОС и лучом, дополнительным к стороне ОС, равен 138 градусам. найдите угол АОС.

1 ответ

Посмотреть ответы

Megamozg

2205

Ответ:
∠АОС = 84°
Объяснение:
Определения:
1. "Дополнительными называются различные лучи, лежащие на одной прямой и имеющие общую граничную точку".
2. "Угол, стороны которого составляют прямую - развернутый угол".
3. "Любой луч, проведенный из вершины развернутого угла, делит его на два угла. Полученные в результате углы имеют одну общую сторону, а две другие составляют прямую. Такие углы называются смежными".
Развернутый угол равен 180°. Угол между биссектрисой ОР угла АОС и лучем, дополнительным к стороне ОС и угол между этой биссектрисой и стороной ОС - смежные углы.
Значит ∠РОС = 180° - 138° = 42°.
∠РОС = ∠АОС : 2, так как ОР - биссектриса.
∠АОС = 2·∠РОС = 2·42 = 84°.

Хороший ответ

4 апреля 2023 15:36

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

В кубе ABCDA1B1C1D1 найдите угол между скрещивающимися упрямыми BB1 и AC. Пожалуйся, очень нужно! Большое спасибо заранее)... В равностороннем треугольнике ABC проведена биссектриса AD. Расстояние от точки D до прямой AC равно 6 сантиметров. Найдите расстояние от вершины A до... В прямоугольном треугольнике ABC с гипотенузой AB и углом A равным 60(градусов), проведена высота CH. Найдите BH, если AH - 6см... Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC = 44, MN = 24. Площадь треугольника ABC... Что значит отношение 5:4...