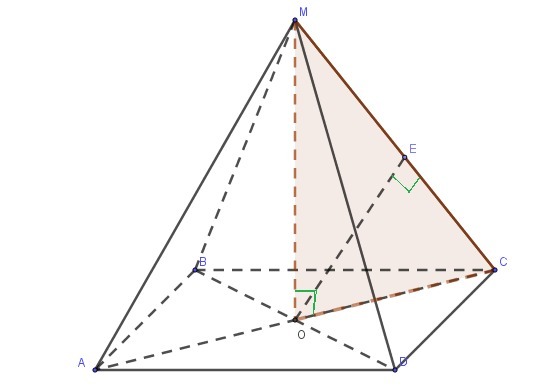
В основании правильной пирамиды MABCD лежит квадрат ABCD. Hайдите расстояние от центра грани ABCD до ребра MC, если высота пирамиды равна 6, а длина ребра MC равна 9

1 ответ

Посмотреть ответы

DevAdmin

1720

О - центр грани ABCD. Расстояние от точки до прямой - длина перпендикуляра, проведенного из данной точки к данной прямой.
OE - расстояние от центра грани ABCD к прямой MC. Поскольку четырехугольная пирамида правильная, то все боковые ребра равны, то есть, MA = MB = MC = MD.

Из прямоугольного треугольника MOC найдем ОС по теореме Пифагора
$\tt MC^2=MO^2+OC^2\\ OC^2=MC^2-MO^2\\ OC^2=9^2-6^2\\ OC^2=45\\ OC=3\sqrt$

Площадь прямоугольного треугольника MOC равна $\tt S=\dfrac$ , а с другой стороны - $\tt S=\dfrac$
Приравнивая площади, получим $\tt OC\cdot MO=OE\cdot MC$ откуда выразим ОЕ
$\tt OE=\dfrac=\dfrac \cdot6}= 2\sqrt$

Ответ: 2√5.

Хороший ответ

4 апреля 2023 17:03

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Площадь основания цилиндра 2 м, а высота 3 м. Найдите диагональ осевого сечения... В треугольнике ABC, AB=BC и BD - биссектриса Найдите 1) угол BCA, если смежный угол при вершине A равен 130 градусов; 2)периметр трегольника ABC, если... Площадь боковой поверхности правильной четырехугольной призмы равна Q.Сечение призмы,проходящее через диагональ нижнего основания и противолезащую вер... P = 2πR что это за формула... Найти номер подчеркнутого члена геометрической прогрессии: -2; -4; …; -64; … НАПИШИТЕ ФОРМУЛУ...