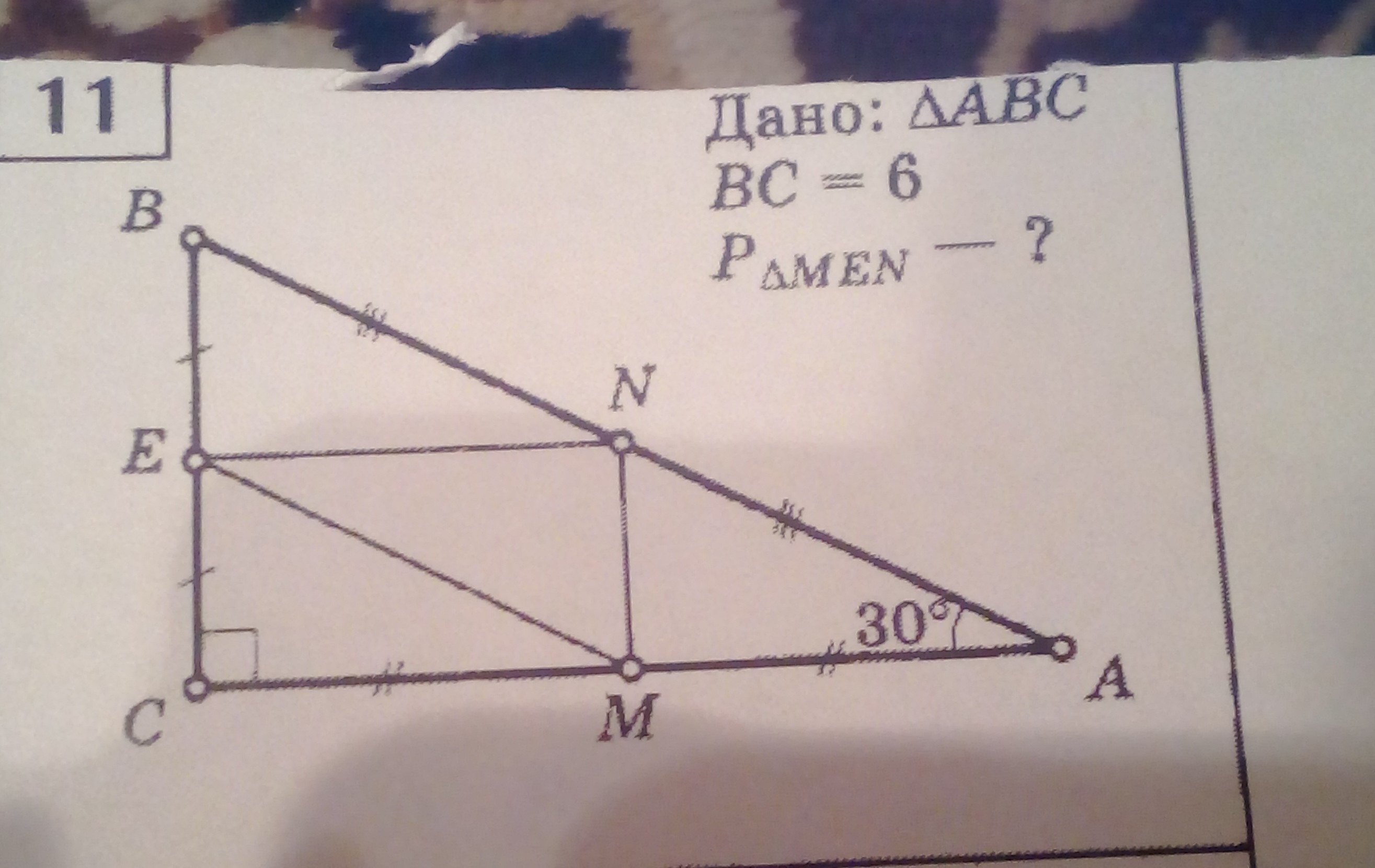
Дано: треугольник ABC , BC=6, Найти:P треугольника men

Решение:
АВ = ВС × 2 = 6 × 2 = 12 (катет лежащий против угла в 30° равен половине гипотинузы)
По теореме Пифагора
ВС² + АС² = АВ²
36 + АС² = 144
АС² = 144 - 36
АС = √108
АС = 6√3
NM, EM и EN - средние линии => стороны образовавшегося ими треугольника равны половинам сторон данного треугольника (по свойству)
Р = 3 + 6 + 3√3 = 9 + 3√3
Ответ: Р = 9 + 3√3

В треугольнике АВС:
АВ = 2ВС = 2*6 = 12 (катет, лежащий против угла 30° равен половине гипотенузы)
АС = √(12²-6²) = √108 = 6√3
Р(АВС) = АВ + ВС +АС = 12 + 6 + 6√3 = 18 + 6√3

EN, EM и MN являются средними линиями треугольника АВС по условию, следовательно
Р(МEN) = P(ABC)/2 = (18+6√3)/2 = (2(9+3√3))/2 = 9 + 3√3

Ответ: 9 + 3√3