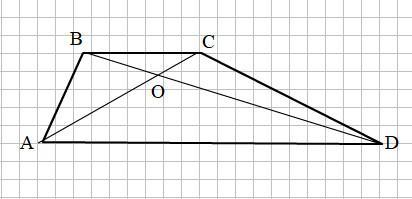
Срочно!!!!Дана трапеция ABCD (AD||BC), диагонали трапеции пересекаются в точке О, SBOC=4см^2, SCOD=8см^2. Найдите площади трапеции.

1 ответ

Посмотреть ответы

DevAdmin

1720

Ответ:
$S_= 36~ cm^$
Объяснение:
Смотри прикреплённый рисунок.
Известно, что диагонали трапеции делят трапецию на 4 треугольника, площади которых находятся в следующем соотношении:
$S_ \cdot S_=S_\cdot S_$ (1)
$S_ = 4~cm^;$
$S_ = 8~cm^;$
Найдём площадь ΔСOD.
$S_{\Delta ABD} = S_{\Delta ACD}$ , так как эти треугольники имеют одно и то же основание AD и одинаковые высоты, равные высоте трапеции.
$S_ = S_ + S_;~~~S_ = S_ + S_;$
Таким образом
$S_ + S_ = S_ + S_;$
$S_ = S_ = 8~cm^$ .
Из соотношения (1) найдём площадь ΔAOD.
$S_= \dfrac\cdot S_}} = \dfrac = 16 ~(cm^ )$
Площадь трапеции ABCD равна
$S_= S_ + S_+S_=S_ = \\\\ = 8 + 4 + 8 + 16 = 36~ (cm^)$

Хороший ответ

4 апреля 2023 20:06

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Угол между плоскостями треугольников ABC и ABD равен 45 (градусов). Треугольник ABC - равносторонний со стороной (4 корня из 3 см), треугольник ABD -... Найдите периметр прямоугольника, если в него вписана окружность радиуса 5. Расписать подробно.... Средняя линия равностороннего треугольника ABC равна 8 см. Найдите периметр этого треугольника.... Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 3 раза?... Напишите уравнение окружности с центром в точке S(2;-1), проходящей через точку B(-3;2)...