Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
2 апреля 2023 23:12
1107
Доказательство (!!!) теоремы о площади равностороннего треугольника.
1
ответ
Площадь равностороннего треугольника находится по формуле
S = a²√3/4, где а - сторона треугольника.
Доказательство:
Проведем ВН - высоту равностороннего треугольника.
Пусть ее длина равна h. Высота в равностороннем треугольнике является и медианой. Тогда АН = НС = а/2.
Площадь треугольника можно найти по формуле
S = a·h/2
Из прямоугольного треугольника АВН по теореме Пифагора выразим высоту через сторону:
h² = a² - (a/2)² = a² - a²/4 = 3a²/4
h = √(3a²/4) = a√3/2
Подставим в формулу площади:
S = (a · a√3/2)/2
S = a²√3/4
Высоту через сторону можно было выразить иначе:
в равностороннем треугольнике углы равны 60°.
Из прямоугольного треугольника АВН по определению синуса:
sin∠A = h/a,
sin60° = √3/2
h = a·sin60° = a√3/2
S = a²√3/4, где а - сторона треугольника.
Доказательство:
Проведем ВН - высоту равностороннего треугольника.
Пусть ее длина равна h. Высота в равностороннем треугольнике является и медианой. Тогда АН = НС = а/2.
Площадь треугольника можно найти по формуле
S = a·h/2
Из прямоугольного треугольника АВН по теореме Пифагора выразим высоту через сторону:
h² = a² - (a/2)² = a² - a²/4 = 3a²/4
h = √(3a²/4) = a√3/2
Подставим в формулу площади:
S = (a · a√3/2)/2
S = a²√3/4
Высоту через сторону можно было выразить иначе:
в равностороннем треугольнике углы равны 60°.
Из прямоугольного треугольника АВН по определению синуса:
sin∠A = h/a,
sin60° = √3/2
h = a·sin60° = a√3/2
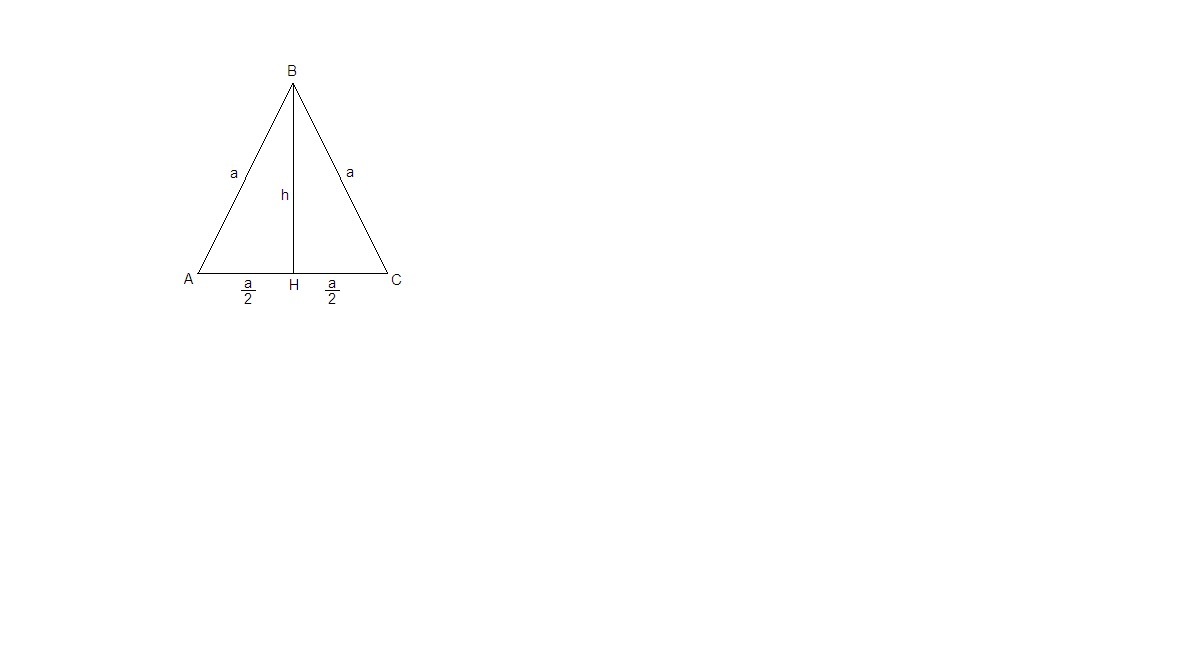
0
·
Хороший ответ
4 апреля 2023 23:12
Остались вопросы?
Еще вопросы по категории Геометрия
В треугольнике ABC известно, что AC = 32, BM - медиана, BM = 23. Найдите AM....
основание трапеции равны 4 и 10.Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей...
Здравствуйте, не могли бы объяснить, как найти периметр многоугольника, если известна площадь и радиус вписанной окружности? просто по действиям, что...
Даны две противоположные вершины квадрата А(3;0) и С(-4; 1). Найти две его другие вершины...
Найдите угол,смежный с углом ABC,если угол 1)ABC=36 градусов 2)угол ABC=102 градуса....