Помогите пожалуйста!!!!!!найдите площадь боковой поверхности пирамиды, все грани которой наклонены к основанию под углом 60 градусов а в основании лежит прямоугольный треугольник с катетами 3 см и 6 см

1 ответ

Посмотреть ответы

Megamozg

2205

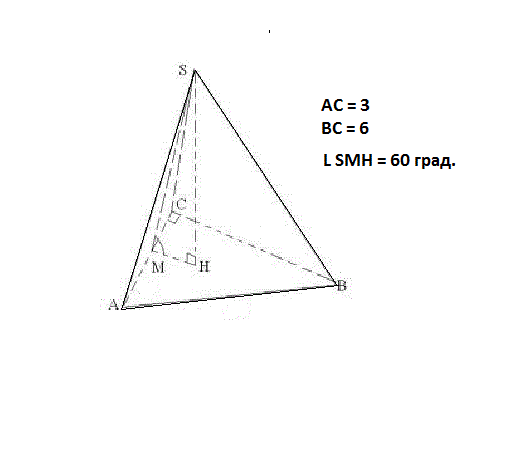
1) площадь боковой пирамиды, у которой рёбра равнонаклоненны к плоскости основания равна половине произведения периметра основания на высоту боковой грани,т.е. S бок = ½·P осн·SM (см. рис.).
2) Найдём периметр основания, для этого вычислим гипотенузу по теореме Пифагора АВ= √ВС²+АС²=√6²+3²=√45=3√5 (см), тогда Р = 9+3√5 (см).
3)Найдём высоту бок. грани из Δ SHM - прям.:
SM= 2·MH= 2·(AC+BC-AB)/2=9-3√5 (cм) (!!!МН - радиус вписанной окружности) .
Тогда S бок = ½·P осн·SM = ½·(9+3√5)(9-3√5)= ½·(81-45)=18 (кв.см.)
Ответ: 18 кв. см..

Хороший ответ

1 сентября 2022 20:29

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Треугольники ABC и ADC лежат в разных плоскостях и имеют общую сторону AC. Точка P – середина стороны AD, точка K – середина DC. 1.Каково взаимное рас... Высота правильной четырехугольной пирамиды равно 8 см, сторона ее основания 12 см. Вычислите длинну бокового ребра пирамиды и площадь боковой поверхно... Дано: KABCDEM - правильная шестиугольная пирамида. КО - высота пирамиды. KT⊥AM; ∠KTO=60°. Найти отношение площадей ΔМКD и ΔMKC.... 1. В треугольнике MNP точка K лежит на стороне MN, причем угол MNP острый. Докажите, что KP< MP. 2. Найдите углы треугольника ABC, если угол B на 4... Высота правильного треугольника равна 90. Найдите радиус окружности, описанной около этого треугольника...