Высота равностороннего треугольника 3см. Найдите радиус описанной около него окружности и радиус вписанной в него окружности.С ЧЕРТЕЖОМ И ПРАВИЛЬНО

Постаралась все объяснить, чтобы вы понимали о чем идет речь

Центр вписанной в треугольник окружности находится в точке пересечении биссектрис треугольника.
Центр описанной окружности находится в точке пересечения срединных перпендикуляров к сторонам треугольника.
Любая точка на биссектрисе равноудалена от сторон угла, в котором она проведена. Точка пересечения биссектрис углов треугольника равноудалена от всех трех его сторон. Биссектриса равностороннего треугольника является и его высотой и медианой.
Так как медианы любого треугольника делятся точкой пересечения в отношении 2:1,
а высоты равностороннего треугольника являются срединными перпендикулярами к его сторонам,
радиус описанной окружности равен расстоянию от точки пересечения высот до вершин треугольника и равен, 2/3 высоты,
а вписанной - расстоянию от точки пересечения биссектрис до сторон треугольника и равен 1/3 высоты правильного треугольника.
Радиус вписанной в данный треугольник окружности равен 3:3= 1см.
Радиус описанной вокруг данного треугольника окружности равен (3:3)*2 см Радиус вписанной окружности в равносторонний треугольник равен одной трети высоты, а радиус описанной - двум третям. Значит, радиус вписанной 1 см, описанной - 2 см.
-----------------------------------
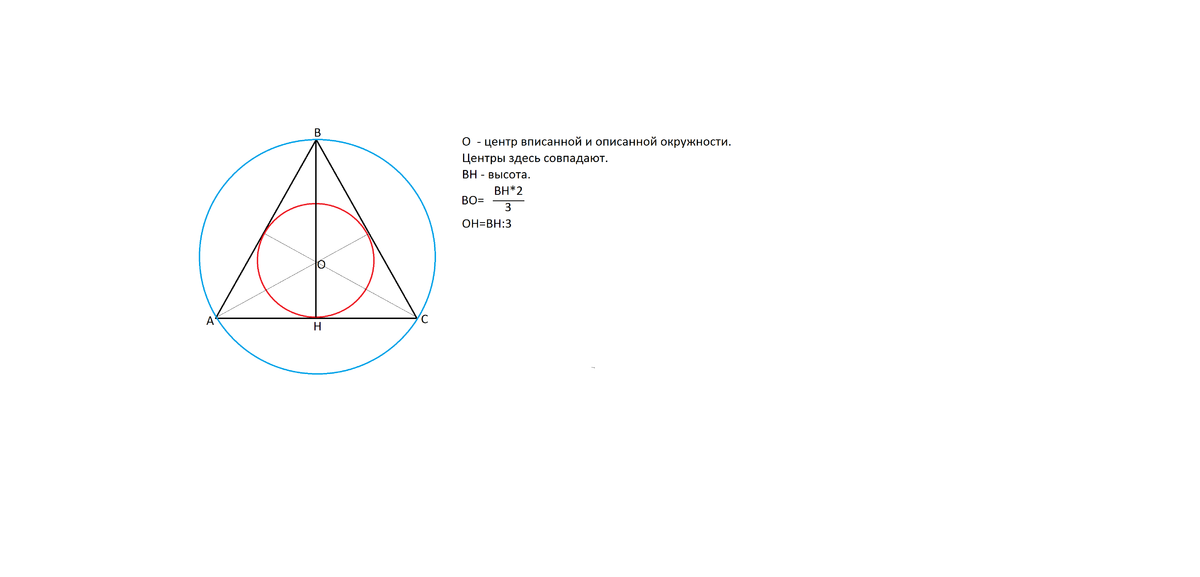
Для решения задачи чертеж не нужен. Но раз учитель требует, даю и чертеж и подробное решение.