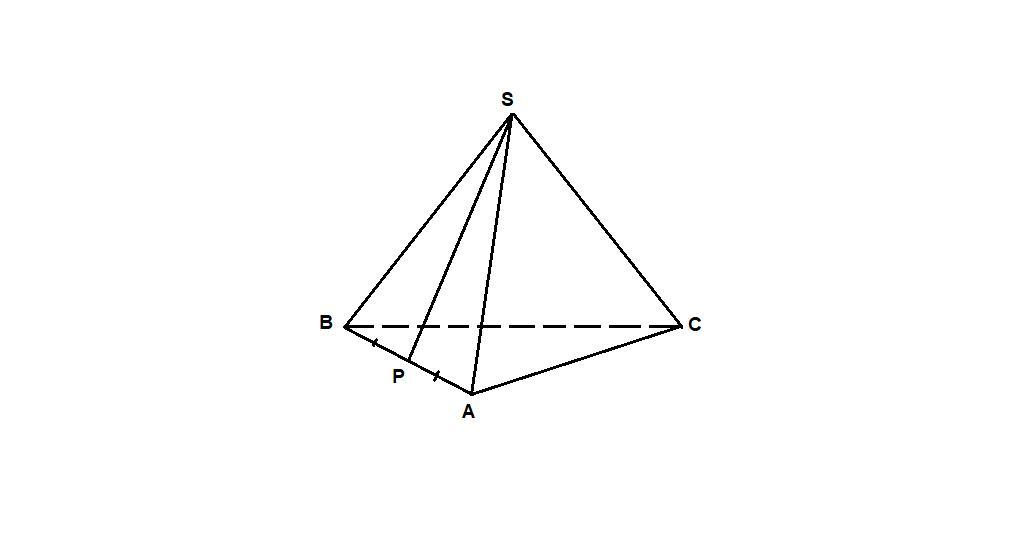
В правильной треугольной пирамиде SABC точка P - середина ребра AB, S-вершина . Известно, что SP=4,а площадь боковой поверхности равна 24. Найдите длину отрезка BC.

1 ответ

Посмотреть ответы

DevAdmin

1690

Ответ:
4
Пошаговое объяснение:
Пирамида правильная, значит основание - правильный треугольник, а боковые грани - равные равнобедренные треугольники.
Площадь боковой поверхности вычисляется по формуле:
$S=\dfracP\cdot l$
где Р - периметр основания,
l - апофема (высота боковой грани)
Тогда $P=\dfrac$
Р - середина АВ, значит SP - медиана и высота ΔSAB, т.е.
SP = 4 - апофема.
$P=\dfrac=12$
BC = P / 3 = 12 / 3 = 4

Хороший ответ

5 апреля 2023 02:57

Остались вопросы?

Найти нужный

Еще вопросы по категории Математика

1 квадратный метр это сколько квадратных дециметров?... Объем параллелепипеда abcda1b1c1d1 равен 72 . найдите объем треугольной пирамиды BCDC1... Какие слова нужно согласовывать по падежу?... Сколько квадратных сантиметров в одном квадратном дециметре?... Разложить рациональное число в конечную цепную дробь а) 19/37 ; б) 49/30 ; в) 81/71 ....