Помогите срочно решить неопределенные интегралы

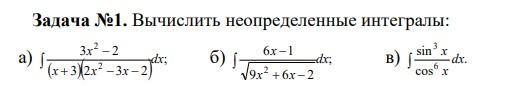
1 ответ

Посмотреть ответы

DevAdmin

1720

Ответ:
1) Интегрирование рациональных дробей .
$\displaystyle \int \frac{(x+3)(2x^2-3x-2)}\, dx=\int \frac{(3x^2-2)\, dx}{(x+3)(2x+1)(x-2)}=(*)$
Разложим на простейшие дроби подынтегральную дробь .
$\displaystyle \frac{(x+3)(2x+1)(x-2)}=\frac+\frac+\frac\ ;\\\\\\3x^2-2=A(2x+1)(x-2)+B(x+3)(x-2)+C(x+3)(2x+1)\ ;\\\\x=-3:\ A=\frac{-5\cdot (-5)}=1\ \ \ ,\ \ \ \ \ x=-\frac:\ B=\frac-2}{\frac\cdot \frac{-5}}=-\frac\\\\\\x=2:\ C=\frac=\frac$

$\displaystyle (*)=\int \Big(\frac-\frac+\frac\Big)\, dx=\\\\\\=\int \frac-\frac\int \frac+\frac\int \frac=\\\\\\=ln|x+3|-\frac\, ln|2x+1|+\frac\, ln|x-2|+C$
2) Интегрирование выражений , содержащих в знаменателе квадратный трёхчлен .

$\displaystyle \int \frac{\sqrt}\, dx=\int \frac{\sqrt{(3x+1)^2-3}}\, dx=\Big[\ t=3x+1\ ,\ x=\frac\ ,\\\\\\dx=\frac\ \Big]=\int \frac{(2t-2)\, dt}}=\frac\int \frac{\sqrt}-\frac\int \frac{\sqrt}=\\\\\\=\frac\cdot 2\sqrt-\frac\cdot ln|\, t+\sqrt\, |+C=\\\\\\=\frac\cdot \sqrt{(3x+1)^2-3}-\frac\cdot ln|\, 3x+1+\sqrt{(3x+1)^2-3}\, |+C=$

$=\dfrac\cdot \sqrt-\dfrac\cdot ln|\, 3x+1+\sqrt\, |+C$

3) Интегрирование тригонометрических выражений .

$\displaystyle \int \frac\, dx=\int \frac=\int \frac{-(1-cos^2x)\cdot d(cosx)}=\\\\\\=\Big[\ t=sinx\ \Big]=\int \frac{(t^2-1)\, dt}=\int \frac-\int \frac=\frac}{-3}-\frac}{-5}+C=\\\\\\=-\frac+\frac+C$

Хороший ответ

5 апреля 2023 03:13

Остались вопросы?

Найти нужный

Еще вопросы по категории Алгебра

Найдите кв корни по дискриминату. Номеи 244 пожалуйста срочно сейчас... Помогите решить. 1+cos(180+a) ____________ sin(180-a) Ответ должен быть tg a/2... Упростите выражение: а) cos 2 a/cos a-sin a б)cos2 B+sin^2 B в)sin B/2 cos^2 B/2... Поезд Омск-Новосибирск отправляется в 18:37,а прибыв.в 3:37 на след.день(вр.московское).Сколько часов поезд находится в пути?... Что это: парабола, гипербола или прямая? y=2x(в квадрате)+x...