Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
3 апреля 2023 03:15
912
Обчислити 1^2-2^2+3^2-4^2+...+99^2-100^2+101^2
1
ответ
Воспользуемся формулой сокращенного умножения, а именно применим разность квадратов.

Заметим, что это арифметическая прогрессия с первым членом a1=1 и разностью прогрессии d=4

Найдем сумму первых 51 членов арифметической прогрессии

ОТВЕТ: 5151.
Заметим, что это арифметическая прогрессия с первым членом a1=1 и разностью прогрессии d=4
Найдем сумму первых 51 членов арифметической прогрессии
ОТВЕТ: 5151.
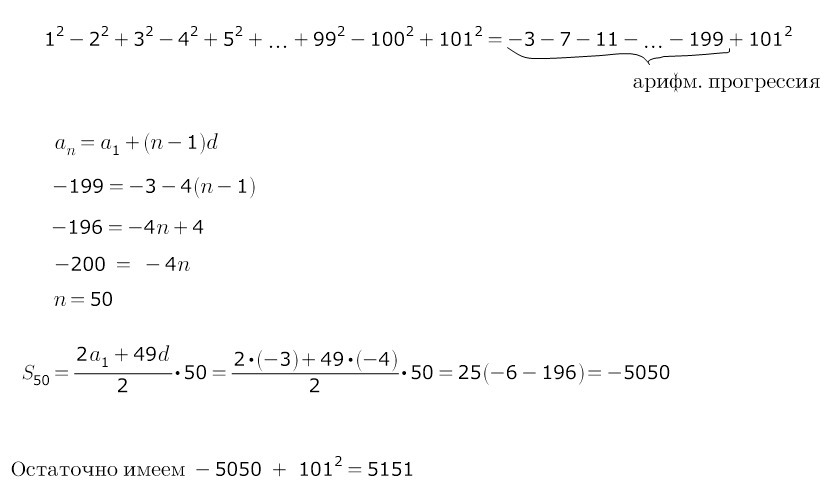
0
·
Хороший ответ
5 апреля 2023 03:15
Остались вопросы?
Еще вопросы по категории Математика
Сколько граммов в одном килограмме?...
Лоску длиной 2 м распилили на части по 5дм сколько частей получилось...
Какие навыки развивает игра "100 плюс минус"?...
Какая физическая величина измеряется в 1 электрон-вольте?...
1)Приведите дроби 3/4,1/2,3/5,3/10,9/20,2/25,9/50 к знаменателю 100 2)Приведите дроби 2/3,1/2,3/4,1/6,4/15,7/20,11/30 к знаменателю 60 Как делать мож...