Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
Каноническое уравнение, задающее эллипс, выглядит так:

Перепишем уравнение эллипса, поменяв местами параметры и
и  :
:

При этом мы получим конгруэнтный эллипс, только повёрнутый в системе координат на 90° (конгруэнтность следует из симметричности канонического уравнения). Поэтому он будет иметь тот же эксцентриситет и то же фокальное расстояние.
Найдём эксцентриситет:

Найдём фокальное расстояние (полурасстояние между фокусами):

Тогда расстояние между фокусами в два раза больше: .
.
Ответ: 6 ед.
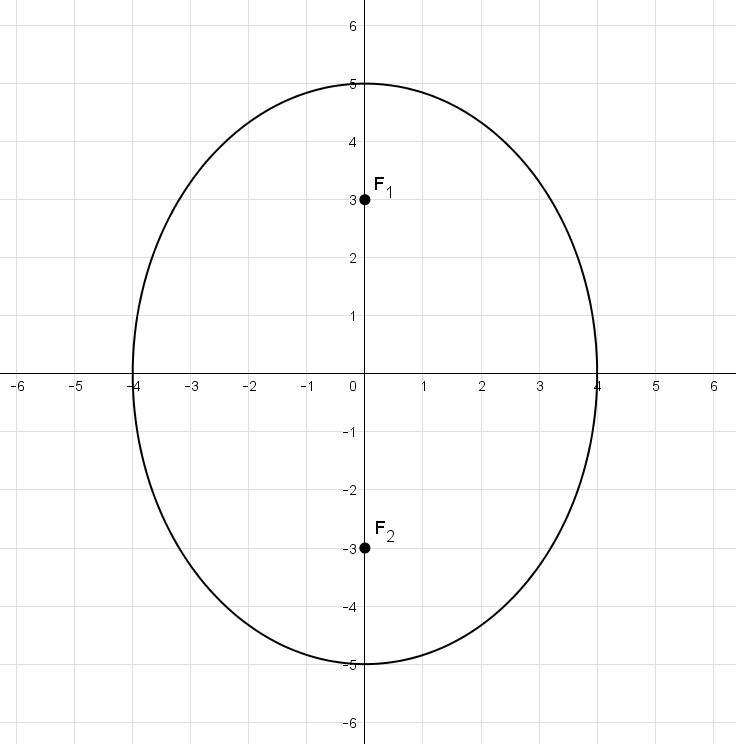
На чертеже изображён данный эллипс. и
и  — его фокусы.
— его фокусы.
Перепишем уравнение эллипса, поменяв местами параметры
При этом мы получим конгруэнтный эллипс, только повёрнутый в системе координат на 90° (конгруэнтность следует из симметричности канонического уравнения). Поэтому он будет иметь тот же эксцентриситет и то же фокальное расстояние.
Найдём эксцентриситет:
Найдём фокальное расстояние (полурасстояние между фокусами):
Тогда расстояние между фокусами в два раза больше:
Ответ: 6 ед.
На чертеже изображён данный эллипс.
0
·
Хороший ответ
5 апреля 2023 04:52
Здесь параметры a = 5 и b = 4.
Фокусное расстояние и полуоси связаны соотношением:
a² = b² + c²
c² = a² - b² = 5² - 4² = 9
Откуда c = 3
Расстояние между фокусами: 2c = 2 * 3 = 6
0
5 апреля 2023 04:52
Остались вопросы?
Еще вопросы по категории Алгебра
Найдите целые решения системы неравенств 10-4x≥3(1-x) 3,5+x<2x 4...
Найти точку пересечения графика функций:у=2х-1,у=5-х...
Упростить 3x -5 + 23x - 9...
Каждое простейшее одноклеточное животное инфузория-туфелька размножается делением на 2 части. Сколько инфузорий стало всего после шестикратного их дел...
Перечислите свойства функции y=g(x), график которой изображен на рисунке 20....