существует ли выпуклый пятиугольник углы которого равны 100°, 110°, 155°, 165°, 200° ответ обоснуйте.

1 ответ

Посмотреть ответы

Megamozg

2205

Ответ:
Не существует!
Объяснение:
По теореме сумма пятиугольник углов любого выпуклого пятиугольника равна 540° (180°(5 - 2)).
Сложим все углы: 100° + 110° + 155°+ 165°+ 200° = 730°. Так как сумма углов больше 540° (730° > 540°), пятиугольник не является выпуклым.
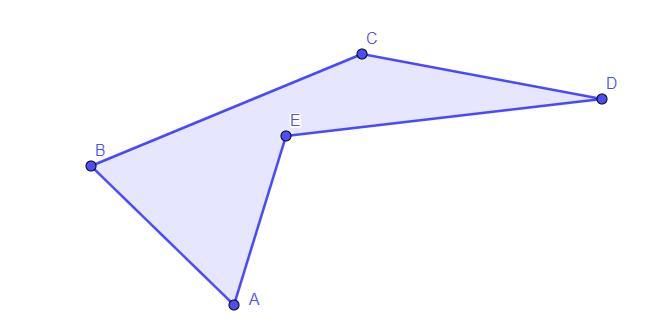
(на рисунке изображен невыпуклый многоугольник)

Хороший ответ

5 апреля 2023 05:20

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Тест 13. Движения   1. Что называется параллельным переносом плоскости на данный вектор? А) Отображение плоскости на себя, при... Помогите пожалуйста, нужно доказать подобность треугольников... Найдите площадь полной поверхности правильной треугольной пирамиды, если ее апофема 4 см, а угол между апофемой и высотой пирамиды равен 30(градусов).... Решите подробно. Соотношение между сторонами и углами в прямоугольном треугольнике. Найдите x... Докажите первый признак равенства треугольников. Какие аксиомы используются при доказательстве теоремы 3.1? Помогите пожалуйста...

существует ли выпуклый пятиугольник углы которого равны 100°, 110°, 155°, 165°, 200° ответ обоснуйте.​

существует ли выпуклый пятиугольник углы которого равны 100°, 110°, 155°, 165°, 200° ответ обоснуйте.