Основания трапеции равны 3 и 2. Диагонали её равны 3 и 4. Найти площадь трапеции.

1 ответ

Посмотреть ответы

DevAdmin

1720

Ответ: 6 (ед. площади)
Объяснение: Способ решения задач на площадь трапеции, в которой известны основания и диагонали, обычно сводится к проведению прямой из вершины при одном основании параллельно диагонали до пересечения с продолжением другого основания и затем вычислением площади получившегося треугольника. .
Подробное решение.
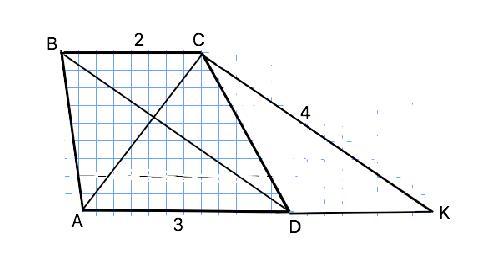
Пусть в трапеции АВСD BC||АD, AD=AC=3, ВС=2, BD=4.
Площадь трапеции равна произведению высоты на полусумму оснований. S(ABCD)=h•(BC+AD):2
Проведем СК||ВD. Тогда ВС||DC, CK|| BD => BCKD - параллелограмм, и DK=BC=2 =>
AK=AD+DK=3+2=5.
Ѕ(∆ АСК)=h•AK:2=S(ABCD)
Вычислив площадь треугольника АСК по т.Герона получим S(ABCD)=S(ACK)=6.
Но конкретно для этой задачи с отношением сторон треугольника АС:СК:АК=3:4:5 проще вычислить площадь треугольника АСК как произведение диагоналей трапеции – этот треугольник прямоугольный ( египетский).
S(ABCD)=S(ACK)= АС•СК:2=3•4:2=6 (ед. площади).

Хороший ответ

5 апреля 2023 06:34

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Биссектриса BD делит сторону AC треугольника ABC на отрезки AD и CD, равные соответственно 7 см и 10,5 см, AB=9 см. Найдите периметр треугольника ABC... Найдите боковую сторону равнобедренного треугольника, если его основание равно 20, а угол при основании равен 30°. Пожалуйста помогите 1)10/√3. 2)10√3... Найти площадь равнобедренного треугольника..если известны периметр - 54 и боковая сторона- 15, в ответе должно получиться - 108... Какие из следующих утверждений верны? 1) у любой трапеции основания параллельны 2) все углы ромба равны 3) Две окружности пересекаются если радиус... Треугольник. Теорема о площади треугольника. Доказательство формулы площади треугольника....