На рисунке изображён график некоторой функции y=f(x). Функция F(x)=−x3+7,5x2−12x+8,5 — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.

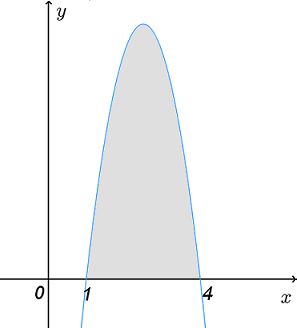
2 ответа

Посмотреть ответы

Megamozg

2190

Площадь данной фигуры равна разности первообразных
S = F(4) - F(1) = (−4^3+7,5* 4^2−12*4+8,5) - (−1^3+7,5*1^2−12*1+8,5) = 13.5 ед^2
Ответ: 13.5 ед^2
Я так понимаю это задание из яндекса, сам его ночью видел. Там есть подробное решение тоже

Хороший ответ

5 апреля 2023 07:54

Megamozg

2190

Найдите площадь закрашенной фигуры.
S = F(x) |[1;4] = −x^3+7,5x^2−12x+8,5 |[1;4] =
= −4^3+7.5*4^2−12*4+8.5 - (−1^3+7.5*1^2−12*1+8.5) =13.5
ОТВЕТ 13.5

5 апреля 2023 07:54

Остались вопросы?

Найти нужный

Еще вопросы по категории Алгебра

Вычислить: 1)sin П/2 + sin 3П/2 2)sin (-П/2) + cos П/2 3)sin П - cos П 4)sin 0 - cos 2П 5)sin П + sin 1,5 П 6)cos 0 - cos 3/2П 1)tg П +соs П 2)tg 0гр... В детский лагерь привезли неизвестное количество ящиков с сухим пайком для юных туристов. Во всех ящиках одинаковое количество упаковок с пайками, при... Смешали 30-%ный раствор соляной кислоты с 10-%ным и получили 600 г 15-%ного раствора. Сколько граммов первого расвора было взято?... 4sin^2x+ tgx = 0 [-2п ; -п]... ЗАДАЧА предприниматель купил здание и собирается открыть в нём отель. В отеле могут быть стандартные номера площадью30 кв. метров и номера "люкс" площ...